CAT 2021 Set-2 | Quantitative Aptitude | Question: 15

Question

For all real values of $x,$ the range of the function $f(x) = \dfrac{x^{2} + 2x + 4}{2x^{2} + 4x + 9}$ is

• A. $ \left(\frac{3}{7}, \frac{1}{2} \right)$
• B. $ \left[\frac{3}{7}, \frac{1}{2} \right)$
• C. $ \left[\frac{3}{7}, \frac{8}{9} \right)$
• D. $ \left[\frac{4}{9}, \frac{8}{9} \right]$

Answer 1

Given that, $f(x) = \dfrac{x^{2} + 2x + 4}{2x^{2} + 4x + 9}; x \in \mathbb{R}$

Let $y = \dfrac{x^{2} + 2x + 4}{2x^{2} + 4x + 9}$

$ \Rightarrow y (2x^{2} + 4x + 9) = x^{2} + 2x + 4$

$ \Rightarrow 2yx^{2} + 4yx + 9y = x^{2} + 2x + 4$

$ \Rightarrow x^{2} (2y-1) + x (4y-2) + 9y – 4 = 0$

For real values of $x,$ discriminant should be greater than equal to zero.

$\Rightarrow D \geq 0$

$ \Rightarrow b^{2} – 4ac \geq 0 \quad [ \because \text{For} \; ax^{2} + bx + c = 0]$

$ \Rightarrow (4y-2)^{2} – 4 (2y-1)(9y-4) \geq 0$

$ \Rightarrow 16y^{2} + 4 – 16y – (8y – 4) (9y – 4) \geq 0$

$ \Rightarrow 16y^{2} – 16y + 4 – (72y^{2} – 32y – 36y + 16) \geq 0$

$ \Rightarrow 16y^{2} – 16y + 4 – 72y^{2} + 68y – 16 \geq 0$

$ \Rightarrow – 56y^{2} + 52y – 12 \geq 0$

$ \Rightarrow 56y^{2} – 52y + 12 \leq 0$

$ \Rightarrow 14y^{2} – 13y + 3 \leq 0$

$ \Rightarrow 14y^{2} – 7y – 6y + 3 \leq 0$

$ \Rightarrow 7y (2y – 1) – 3 (2y – 1) \leq 0$

$ \Rightarrow (2y – 1) (7y – 3) \leq 0$



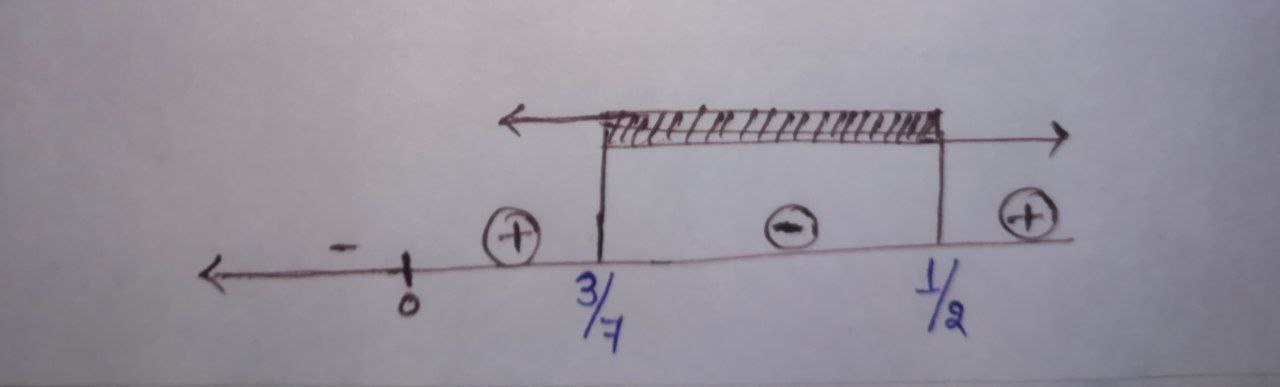
$\boxed{ y \in \left[ \frac{3}{7}, \frac{1}{2} \right]}$

$\therefore$ The range of the function is $\left[ \dfrac{3}{7}, \dfrac{1}{2} \right).$

Correct Answer $: \text{B}$