CAT 2021 Set-3 | Quantitative Aptitude | Question: 6

Question

Let $\text{ABCD}$ be a parallelogram. The lengths of the side $\text{AD}$ and the diagonal $\text{AC}$ are $10 \; \text{cm}$ and $20 \; \text{cm},$ respectively. If the angle $\angle \text{ADC}$ is equal to $30^{\circ}$ then the area of the parallelogram, in sq. cm, is

• A. $\frac{25(\sqrt{5} + \sqrt{15})}{2}$
• B. $25 (\sqrt{5} + \sqrt{15})$
• C. $\frac{25 (\sqrt{3} + \sqrt{15})}{2}$
• D. $25 (\sqrt{3} + \sqrt{15})$

Answer 1

Let’s draw the parallelogram.

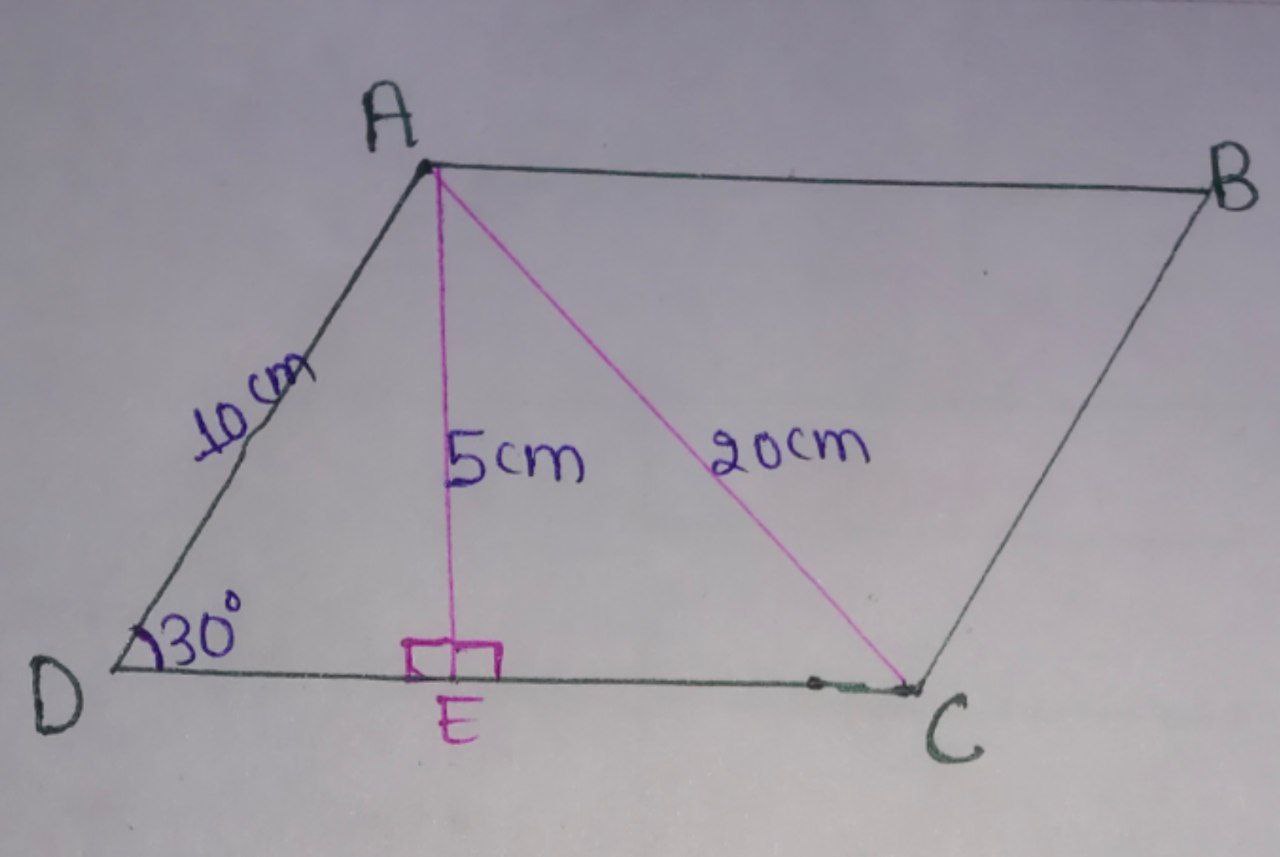
Let $\text{AE}$ be the height of the parallelogram.

In $\triangle \text{AED},$

$\Rightarrow \text{sin} \; 30^{\circ} = \frac{\text{AE}}{\text{AD}}$

$\Rightarrow \frac{1}{2} = \frac{\text{AE}}{10}$

$\Rightarrow \boxed{\text{AE} = 5 \;\text{cm}}$

In $\triangle \text{AED},$ apply the Pythagorean theorem.

$\text{(Hypotenuse)}^{2} = \text{(Perpendicular)}^{2} + \text{(Base)}^{2}$

$\Rightarrow 10^{2} = 5^{2} + \text{(DE)}^{2}$

$\Rightarrow \text{DE} = \sqrt{100-25} = \sqrt{75}$

$\Rightarrow \boxed{\text{DE} = 5 \sqrt{3} \; \text{cm}}$

In $\triangle \text{AEC},$ apply the Pythagorean theorem.

$\Rightarrow 20^{2} = 5^{2} + \text{(EC)}^{2}$

$\Rightarrow \text{(EC)}^{2} = 400-25 = 375$

$\Rightarrow \text{EC} = \sqrt{375}$

$\Rightarrow \boxed{\text{EC} = 5\sqrt{15} \; \text{cm}}$

So, the length of $\text{DC} = \text{DE} + \text{EC}$

$\Rightarrow \boxed{\text{DC} = (5\sqrt{3} + 5\sqrt{15}) \; \text{cm}}$

The area of parallelogram $\text{ABCD} = \text{Base} \times \text{Height} = \text{DC} \times \text{AE}$

$ \qquad \qquad \qquad = (5\sqrt{3} + 5\sqrt{15}) \times 5 = 25(\sqrt{3} + \sqrt15) \; \text{cm}^{2}$

$\therefore$ The area of parallelogram $\text{ABCD}$ is $25(\sqrt{3} + \sqrt15) \; \text{cm}^{2}.$

Correct Answer $:\text{D}$