Let the length of the diagonal of a rhombus be $2a$ meter, $2b$ meter.
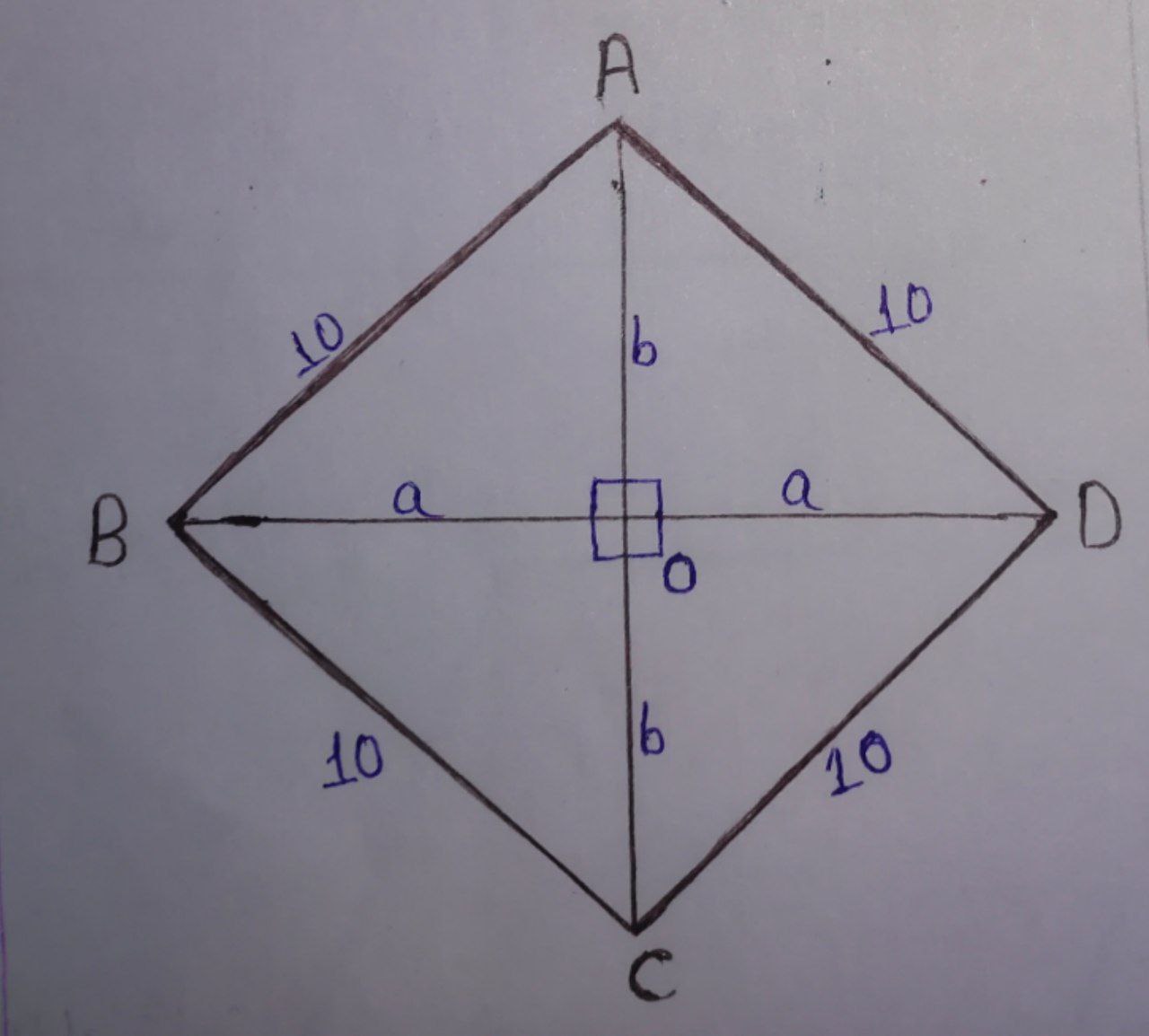
Area of the rhombus $= \dfrac{\text{Product of diagonal}}{2}$
$\Rightarrow 96 = \frac{2a \times 2b}{2}$
$\Rightarrow \boxed{ab = 48}$
In $\triangle \text{AOB},$ we can apply the Pythagorean theorem.
$\text{Hypotenuse}^{2} = \text{Perpendicular}^{2} + \text{Base}^{2}$
$\Rightarrow \text{AB}^{2} = \text{OA}^{2} + \text{OB}^{2}$
$\Rightarrow 10^{2} = a^{2} + b^{2}$
$\Rightarrow \boxed{a^{2} + b^{2} = 100}$
Now, $(a+b)^{2} – 2ab =100$
$\Rightarrow (a+b)^{2} – 96 =100 \quad [\because ab=48]$
$\Rightarrow (a+b)^{2} =196$
$\Rightarrow \boxed{a+b =14} \; \longrightarrow (1)$
And $(a-b)^{2} + 2ab =100$
$\Rightarrow (a-b)^{2}+96 =100$
$\Rightarrow (a-b)^{2} =4$
$\Rightarrow \boxed{a-b =2} \; \longrightarrow (2)$
Adding the equation $(1)$, and equation $(2).$
$ \qquad \require{cancel} \begin{array} {} a+\cancel{b} = 14 \\ a-\cancel{b} = 2 \\\hline 2a \quad = 16 \end{array}$
$\Rightarrow \boxed{a=8}$
From equation $(1),$
$\Rightarrow a+b=14$
$\Rightarrow 8+b=14$
$\Rightarrow \boxed{b=6}$
So,
- The length of the one diagonal $=2a=16$ meters.
- The length of the other diagonal $=2b=12$ meters.
$\therefore$ The cost in INR, of laying electric wires along its two diagonal at the rate of ₹$125$ per meter $=28 \times 125= \text{₹}3500.$
Correct Answer $:3500$