Let’s draw the trapezium for better understanding.
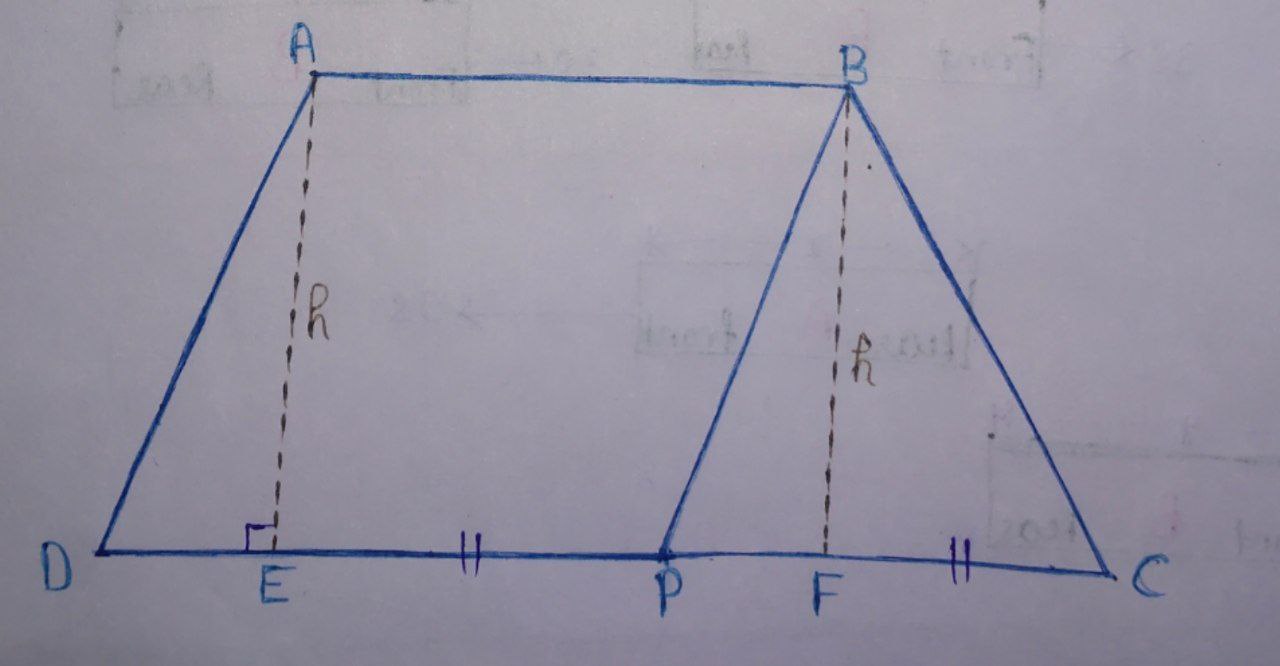
Let $\text{PD} = a \; \text{cm} \Rightarrow \text{PC} = a \; \text{cm} \Rightarrow \text{CD} = 2a \; \text{cm}$
Area of the parallelogram $\text{ABPD}= a \times h \; \text{cm}^{2}$
Area of $\triangle \text{BPC} = \frac{1}{2} \times a \times h \; \text{cm}^{2}$
Now, $ah – \frac{1}{2}ah = 10$
$ \Rightarrow 2ah – ah = 20$
$ \Rightarrow \boxed{ah = 20 \; \text{cm}^{2}}$
$\therefore$ Area of the trapezium $\text{ABCD} = \frac{1}{2} (a + 2a) \times h$
$\qquad \qquad = \frac{1}{2} \times 3ah = \frac{1}{2} \times 3(20) = 30 \; \text{cm}^{2}.$
Correct Answer $: \text{B}$
$\textbf{PS:}$ A trapezium, also known as a trapezoid, is a quadrilateral in which a pair of sides are parallel, but the other pair of opposite sides are non-parallel. The area of a trapezium is computed with the following formula:
$$\text{Area}=\frac {1}{2} × \text {Sum of parallel sides} × \text{Distance between them}.$$

The parallel sides are called the bases of the trapezium. Let $b_1$ and $b_2$ be the lengths of these bases. The distance between the bases is called the height of the trapezium. Let $h$ be this height. Then this formula becomes:
$$\boxed{\text{Area}=\frac{1}{2}(b_1+b_2)h}$$