Ans is option (C)
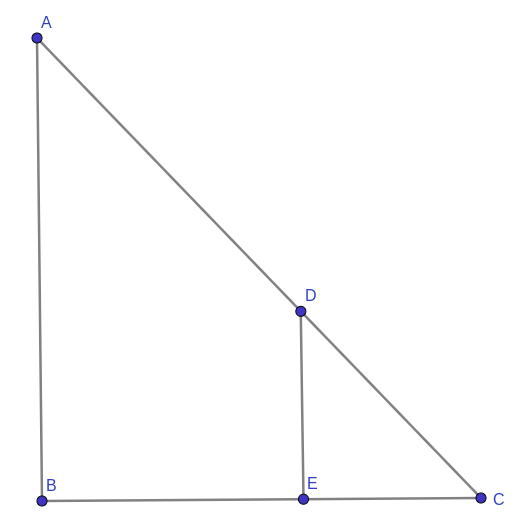
In the figure, the man’s height i.e. length of segment $DE=1.4m$
Length of the man’s shadow i.e. length of segment $EC=1.2m$
Height of the tower i.e. length of segment $AB=h$ mtr
Length of tower’s shadow i.e. length of segment $BC=5.4m$
$\therefore$ $tanC=\frac{DE}{EC}=\frac{AB}{BC}$
$\Rightarrow$ $\frac{1.4}{1.2}=\frac{h}{5.4}$
$\Rightarrow$ $h=6.3m$