Given that, $\text{ABCD}$ be a rectangle inscribed in a circle of radius $13\;\text{cm.}$
Let the length and breadth of the rectangle be $l$ and $b$ respectively.
We can draw the diagram,
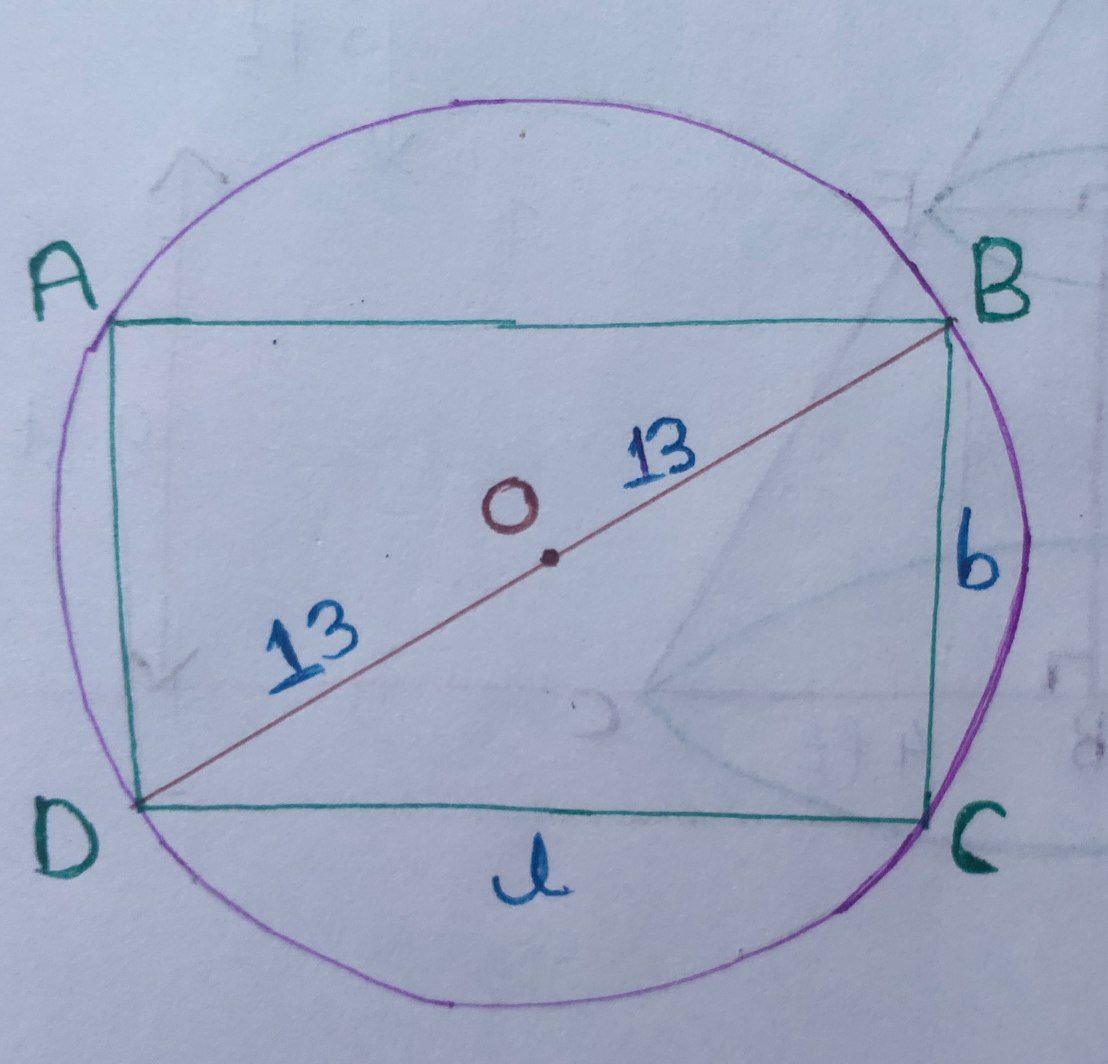
The rectangle $\text {ABCD}$ is inside the circle.
So, the diameter of the circle is equal to the diagonal of the rectangle.
In $\triangle \text{BCD},$ apply the Pythagoras’ theorem,
$ \text{(BD)}^{2} = \text{(BC)}^{2} + \text{(CD)}^{2}$
$ \Rightarrow (26)^{2} = b^{2} + l^{2}$
$ \Rightarrow b^{2} + l^{2} = 676 \quad \longrightarrow (1)$
Now, check all the options,
- $l=24, b=10$
From equation $(1),$ we get
$b^{2} + l^{2} = 676$
$ \Rightarrow (10)^{2} + (24)^{2} = 676$
$ \Rightarrow 100 + 576 = 676$
$ \Rightarrow \boxed{676 = 676}$ (Satisfied)
- $l=25, b=9 $
From equation $(1),$ we get
$b^{2} + l^{2} = 676$
$ \Rightarrow (9)^{2} + (25)^{2} = 676$
$ \Rightarrow 81 + 625 = 676$
$ \Rightarrow \boxed {706 \neq 676} $ ( Not satisfied)
- $l=24, b=12 $
From equation $(1),$ we get
$b^{2} + l^{2} = 676$
$ \Rightarrow (12)^{2} + (24)^{2} = 676$
$ \Rightarrow 144 + 576 = 676$
$ \Rightarrow \boxed {720 \neq 676}$ ( Not satisfied)
- $l=25, b=10 $
From equation $(1),$ we get
$b^{2} + l^{2} = 676$
$ \Rightarrow (10)^{2} + (25)^{2} = 676$
$ \Rightarrow 100+ 625 = 676$
$ \Rightarrow \boxed{725 \neq 676}$ ( Not satisfied)
$ \therefore$ The length of the rectangle $l = 24\; \text{cm},$ and the breadth of the rectangle $b = 10\; \text{cm}.$
Correct Answer $ : \text {A}$