Given that, in a parallelogram $\text{ABCD}$ of area $72$ sq cm, the sides $\text{CD}$ and $\text{AD}$ have lengths $9$ cm and $16$ cm, respectively.
Let $‘h\text{’ cm}$ be the height.
We can draw the parallelogram,
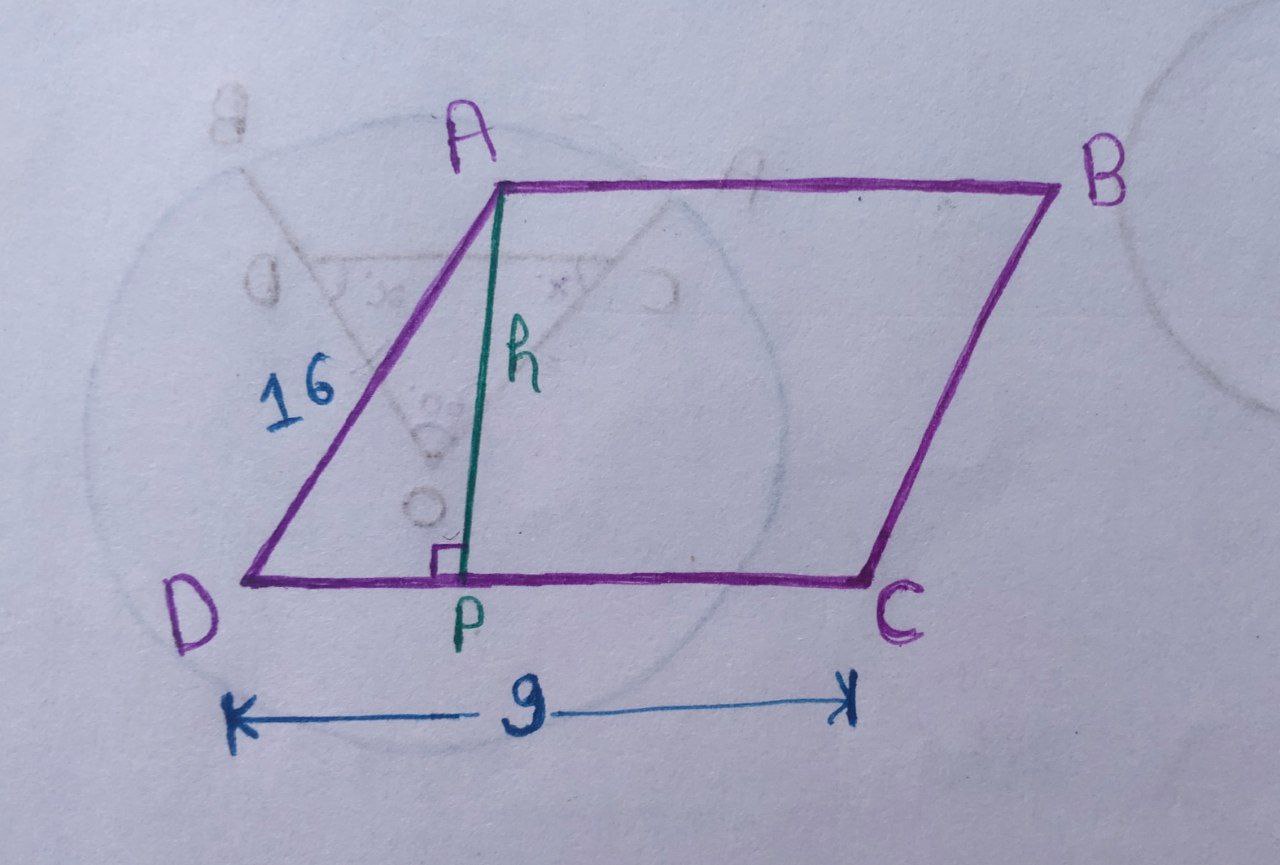
We know that, the area of the parallelogram $ = \text{Base} \times \text{Height}$
Thus, $ 9 \times h = 72 $
$ \Rightarrow \boxed{h = 8\;\text{cm}}$
In $\triangle \text{APD}$, apply the Pythagoras’ theorem,
$ \text{(AD)}^{2} = \text{(AP)}^{2} + \text{(DP)}^{2}$
$ \Rightarrow 8^{2} + \text{(DP)}^{2} = (16)^{2}$
$ \Rightarrow \text{(DP)}^{2} = 256 – 64$
$ \Rightarrow \text{(DP)}^{2} = 192$
$ \Rightarrow \text{DP} = \sqrt{192}$
$ \Rightarrow \text{DP} = \sqrt{64 \times 3} $
$ \Rightarrow \text{DP} = 8 \sqrt{3} \; \text{cm}$
$ \therefore$ The area of triangle $ \text{APD}= \frac{1}{2} \times \text{Base} \times \text{Height}$
$ \quad = \frac{1}{2} \times 8 \sqrt{3} \times 8$
$\quad = 32 \sqrt{3} \; \text{cm}^{2}$
Correct Answer $ : \text{C}$