Given that,
- $ \left | x \right | + \left | y \right | \leq 2 \quad \longrightarrow (1) $
- $ \left | x \right | \geq 1 \quad \longrightarrow (2) $
We know that, $ \left | x \right | = \left\{\begin{matrix} x \; ; & x \geq 0 & \\ -x\; ; & x < 0 & \end{matrix}\right.$
Now, from the equation $(1),$
- $ x+y = 2 \quad \longrightarrow (3) $
- $ x-y = 2 \quad \longrightarrow (4) $
- $ -x+y = 2 \quad \longrightarrow (5) $
- $ -x-y = 2 \quad \longrightarrow (6) $
On solving equation $(3)$, and $(4),$ we get
$\begin{array}{c} x+y = 2 \\ x-y = 2 \\\hline 2x = 4 \end{array}$
$ \Rightarrow x=2,$ and $y=0$
$ \Rightarrow \boxed{(x,y) = (2,0)}$
On solving equation $(3)$, and $(5),$ we get
$\begin{array}{c} x+y = 2 \\ -x+y = 2 \\\hline 2y = 4 \end{array}$
$ \Rightarrow y=2,$ and $x=0$
$ \Rightarrow \boxed{(x,y) = (0,2)}$
On solving equation $(4)$, and $(6)$, we get
$\begin{array}{c} x-y = 2 \\ -x-y = 2 \\\hline -2y = 4 \end{array}$
$ \Rightarrow y=-2,$ and $x=0$
$ \Rightarrow \boxed{(x,y) = (0,-2)}$
On solving equation $(5)$, and $(6)$, we get
$\begin{array}{c} -x+y = 2 \\ -x-y = 2 \\\hline -2x = 4 \end{array}$
$ \Rightarrow x=-2,$ and $y=0$
$ \Rightarrow \boxed{(x,y) = (-2,0)}$
Now, from the equation $(2),$
- $ x=1 \quad \longrightarrow (7)$
- $ -x=1 \Rightarrow x=-1 \quad \longrightarrow (8)$
Put $\boxed {x=1}$ in equation $(3)$, and $(4)$, we get
- $ x+y = 2 \Rightarrow 1+y = 2 \Rightarrow \boxed{y=1}$
$ \qquad \qquad \qquad \Rightarrow \boxed{(x,y) = (1,1)}$
- $ x-y = 2 \Rightarrow 1-y = 2 \Rightarrow \boxed{y=-1}$
$ \qquad \qquad \qquad \Rightarrow \boxed{(x,y) = (1,-1)}$
Put $ \boxed {x=-1}$ in equation $(5)$, and $(6)$, we get
- $ -x+y = 2 \Rightarrow -(-1)+y = 2 \Rightarrow \boxed{y=1}$
$ \qquad \qquad \qquad \Rightarrow \boxed{(x,y) = (-1,1)}$
- $ -x-y = 2 \Rightarrow -(-1)-y = 2 \Rightarrow \boxed{y=-1}$
$ \qquad \qquad \qquad \Rightarrow \boxed{(x,y) = (-1,-1)}$
Now, we can draw the $x\text{-}y$ plane.
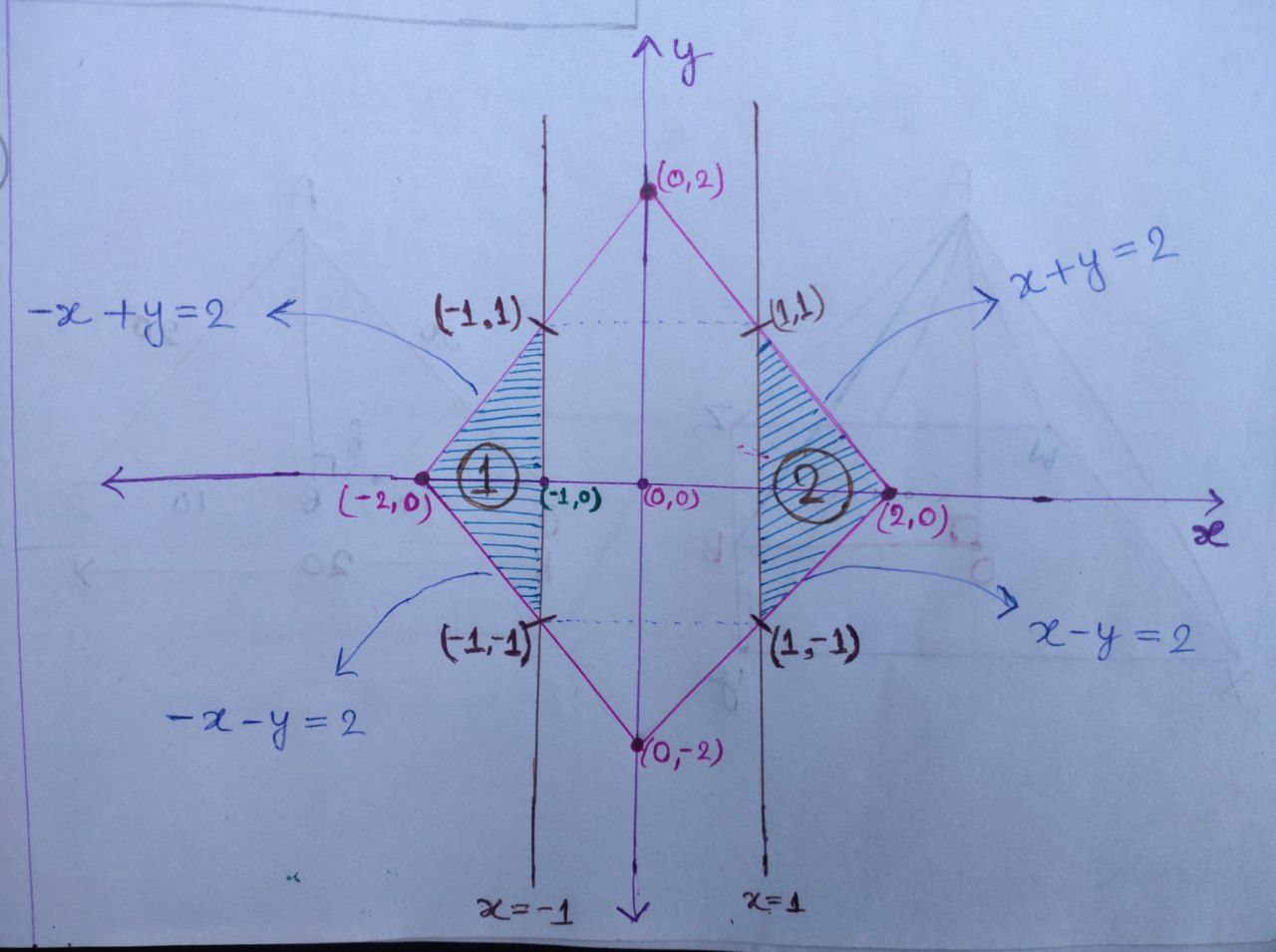
We know that, area of triangle $ = \frac{1}{2} \times \text{Base} \times \text{Height}$
Here, area of shaded triangle $ 1 = 2 \left( \frac{1}{2} \times 1 \times 1 \right) = 1 \; \text {square unit} $
And, area of shaded triangle $ 2= 2 \left( \frac{1}{2} \times 1 \times 1 \right) = 1 \; \text {square unit} $
The total area of the region represented by $S =$ area of shaded triangle $1 +$ area of shaded triangle $2$
$\qquad = 1+1 = 2 \; \text {square units} $
$\therefore$ The total area of the region represented by $S$ is $2 \; \text {square units.} $
Correct Answer $:2$