Given that, corners are cut from an equilateral triangle to produce a regular convex hexagon. The smaller triangles cut are equilateral triangles (If we cut off corners to create a regular hexagon, then each angle of the hexagon is $120^{\circ}$, and so each angle of every removed triangle is $60^{\circ}$ making these triangles equilateral)
Let the original triangle side be $3a.$
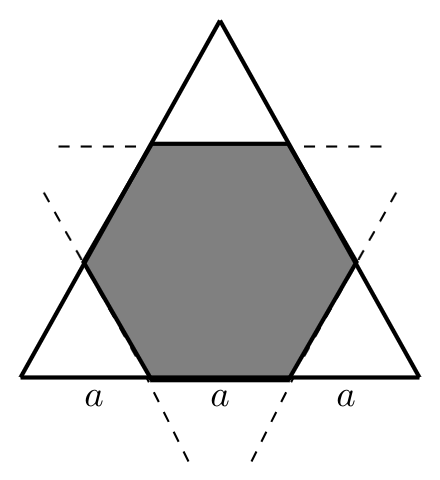
The area of regular convex hexagon $H = \frac{3\sqrt{3}}{2}s^{2},$ the area of equilateral triangle $ T= \frac{\sqrt{3}}{4}s^{2},$ where $s$ is the side length.
Now, $H_{1} = \frac{3\sqrt{3}}{2}a^{2},T_{1} = \frac{\sqrt{3}}{4}(3a)^{2} = \frac{9\sqrt{3}}{4}a^{2}$
The required ratio $ = \dfrac{H_{1}}{T_{1}} = \dfrac{\frac{3\sqrt{3}}{2}a^{2}}{\frac{9\sqrt{3}}{4}a^{2}} = \frac{2}{3}.$
$\therefore$ The ratio of the area of the regular convex hexagon to the area of the original equilateral triangle is $2:3.$
Correct Answer $:\text{D}$