Given that, the area of rhombus $= 12\; \text{cm}^{2},$ and side length $= 5\;\text{cm.}$
Let the diagonal length of the rhombus be $2a\;\text{cm},\;2b\;\text{cm}, (a>b)$
Let’s draw the diagram.
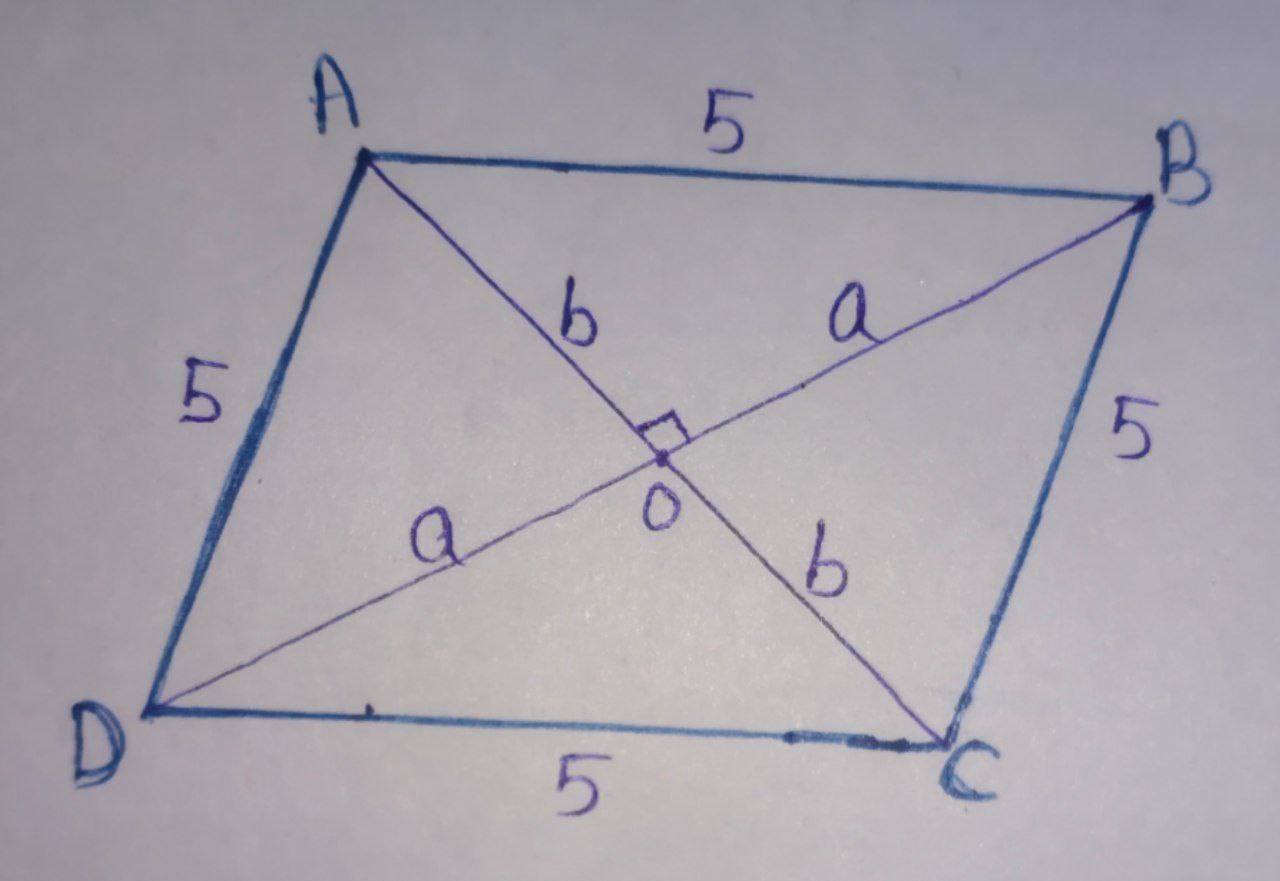
$\triangle \text{AOB}$ is a right-angle triangle. We can apply the Pythagorean theorem.
$\text{(Hypotenuse)}^{2} = \text{(Perpendicular)}^{2} + \text{(Base)}^{2}$
$\Rightarrow 5^{2} = a^{2} + b^{2}$
$\Rightarrow \boxed{a^{2} + b^{2} = 25}\quad \longrightarrow (1)$
The area of rhombus $= \dfrac{\text{Product of diagonal}}{2}$
$\Rightarrow 12 = \frac{2a \times 2b}{2}$
$\Rightarrow \boxed{ab = 6}$
From equation $(1),$
$a^{2} + b^{2} = 25$
$\Rightarrow (a+b)^{2} – 2ab = 25$
$\Rightarrow (a+b)^{2} – 2(6) = 25\quad [\because ab=6]$
$\Rightarrow (a+b)^{2} = 25 + 12$
$\Rightarrow (a+b)^{2} = 37$
$\Rightarrow \boxed{a+b = \sqrt{37}}\quad \longrightarrow (2)$
Again, from equation $(1),$
$a^{2} + b^{2} = 25$
$\Rightarrow (a-b)^{2} + 2ab = 25$
$\Rightarrow (a-b)^{2} + 2(6) = 25\quad [\because ab=6]$
$\Rightarrow (a-b)^{2} = 25 - 12$
$\Rightarrow (a-b)^{2} = 13$
$\Rightarrow \boxed{a-b = \sqrt{13}}\quad \longrightarrow (3)$
Adding the equation $(2)$ and $(3).$
$\begin{array}{} a+b = \sqrt{37} \\ a-b = \sqrt{13} \\\hline \end{array}$
$\boxed{2a = \sqrt{37} + \sqrt{13}}$
Subtract the equation $(3),$ from equation $(2).$
$\begin{array}{} a+b = \sqrt{37} \\ a-b = \sqrt{13} \\ – \;\;\; + \qquad – \\\hline \end{array}$
$\boxed{2b = \sqrt{37} - \sqrt{13}}$
$\therefore$ The length of the longer diagonal $= 2a = (\sqrt{37} + \sqrt{13})\;\text{cm.}$
Correct Answer $:\text{B}$