Given that, radius of circle $ = 5 \; \text{m}.$
Now, using the given information we can draw the diagram.
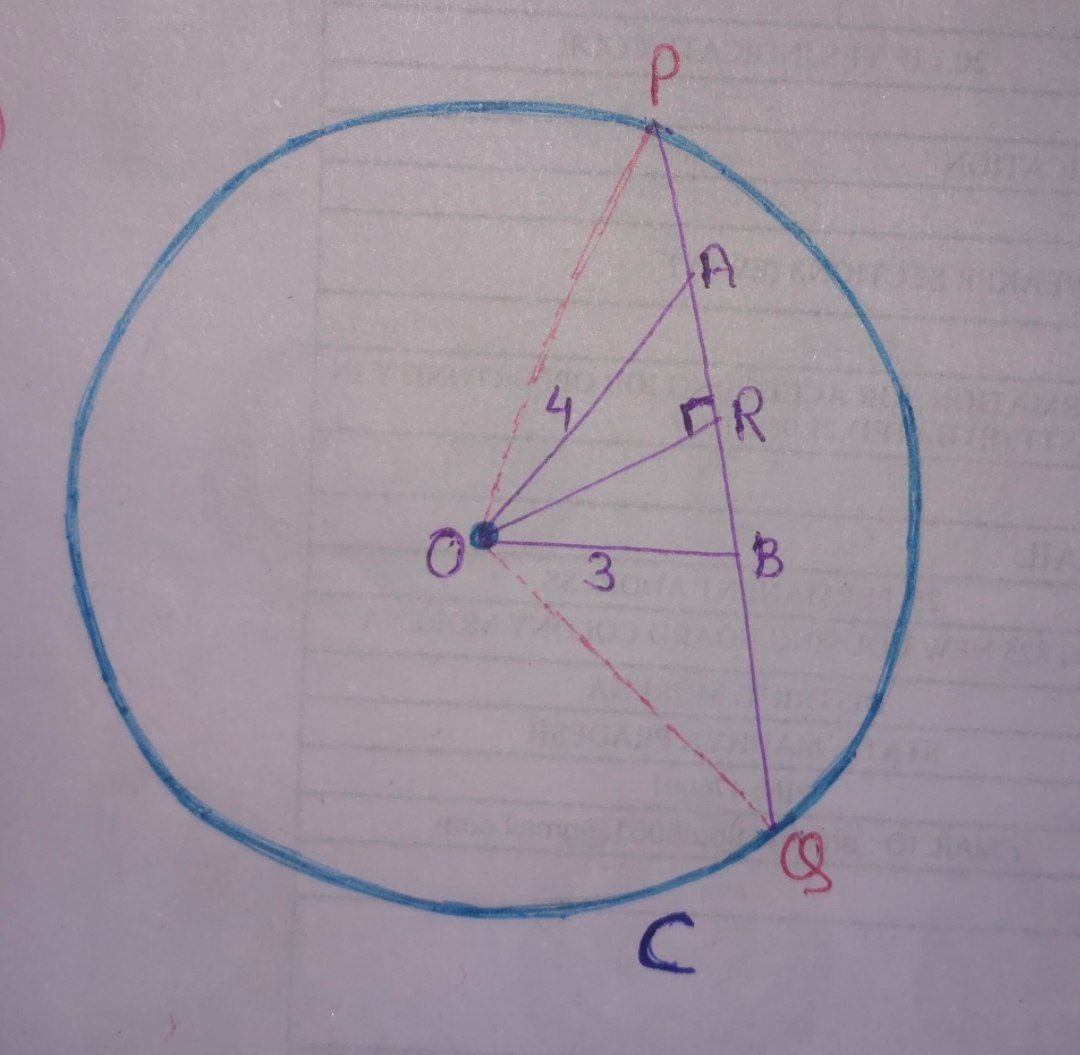
In $\triangle \text{AOB} :$
$\frac{1}{2} \times 4 \times 3 = \frac{1}{2} \times 5 \times \text{OR}$
$ \Rightarrow \boxed{ \text{OR} = 2 .4 \; \text{m}} $
$\text{OR}$ bisects chord $\text{PQ} \Rightarrow \boxed{ \text{PR = RQ}} $
Now, we can take out $\triangle \text{ORP},$ and observe.
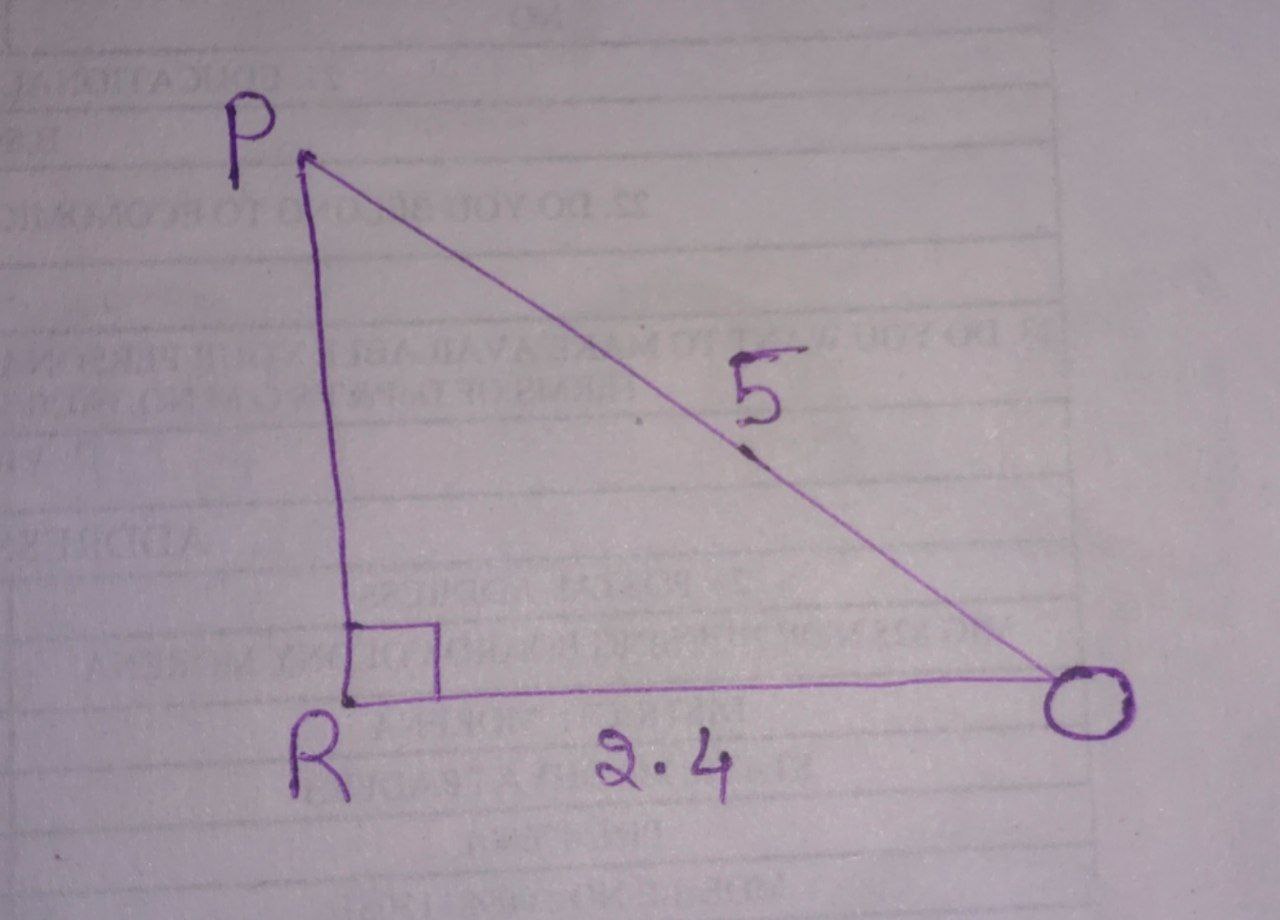
Using the Pythagorean theorem $:$
$\text{(OP)}^{2} = \text{(PR)}^{2} + \text{(OR)}^{2} $
$ \Rightarrow (5)^{2} = \text{(PR)}^{2} +(2 .4)^{2} $
$ \Rightarrow 25 = \text{(PR)}^{2} + 5 .76 $
$ \Rightarrow \text{(PR)}^{2} = 25 – 5 .76 $
$ \Rightarrow \text{PR} = \sqrt{ 25 – 5 .76} $
$ \Rightarrow \text{PR} = \sqrt{19 .24} $
$ \Rightarrow \boxed{\text{PR} = 4 .39 \; \text{m}} $
Thus, $\text{PQ} = \text{PR} + \text{RQ} $
$ \Rightarrow \text{PQ} = \text{PR} + \text{PR} \quad [\because \text{PR = RQ}] $
$ \Rightarrow \text{PQ} = 2 \text{PR} $
$ \Rightarrow \text{PQ} = 2 (4 .39) $
$ \Rightarrow \text{PQ} = 8 .78 \; \text{m} $
$ \Rightarrow \boxed{\text{PQ} \approx 8 .8 \; \text{m}} $
$\therefore$ The length of $\text{PQ} \; \text{in meters},$ is nearest to $8 .8.$
Correct Answer$: \text{D}$