Let the cost price (purchase price) of desktop and laptop be $x$ and $y$ respectively.
Now, $x + y = 50000 \quad \longrightarrow (1)$
And, $ \frac{120}{100}x + \frac{90}{100}y = \frac{102}{100} \times 50000$
$ \Rightarrow 12x + 9y = 102 \times 5000$
$ \Rightarrow 12x + 9y = 510000$
$ \Rightarrow 12x + 9(50000 – x) = 510000 \quad [\because \text{From equation} (1)]$
$ \Rightarrow 12x + 450000 – 9x = 510000$
$ \Rightarrow 3x = 60000$
$ \Rightarrow \boxed{x = 20000} $
$\therefore$ The purchase price of the desktop is $₹ 20000.$
$\textbf{Short Method:}$ Using alligation method
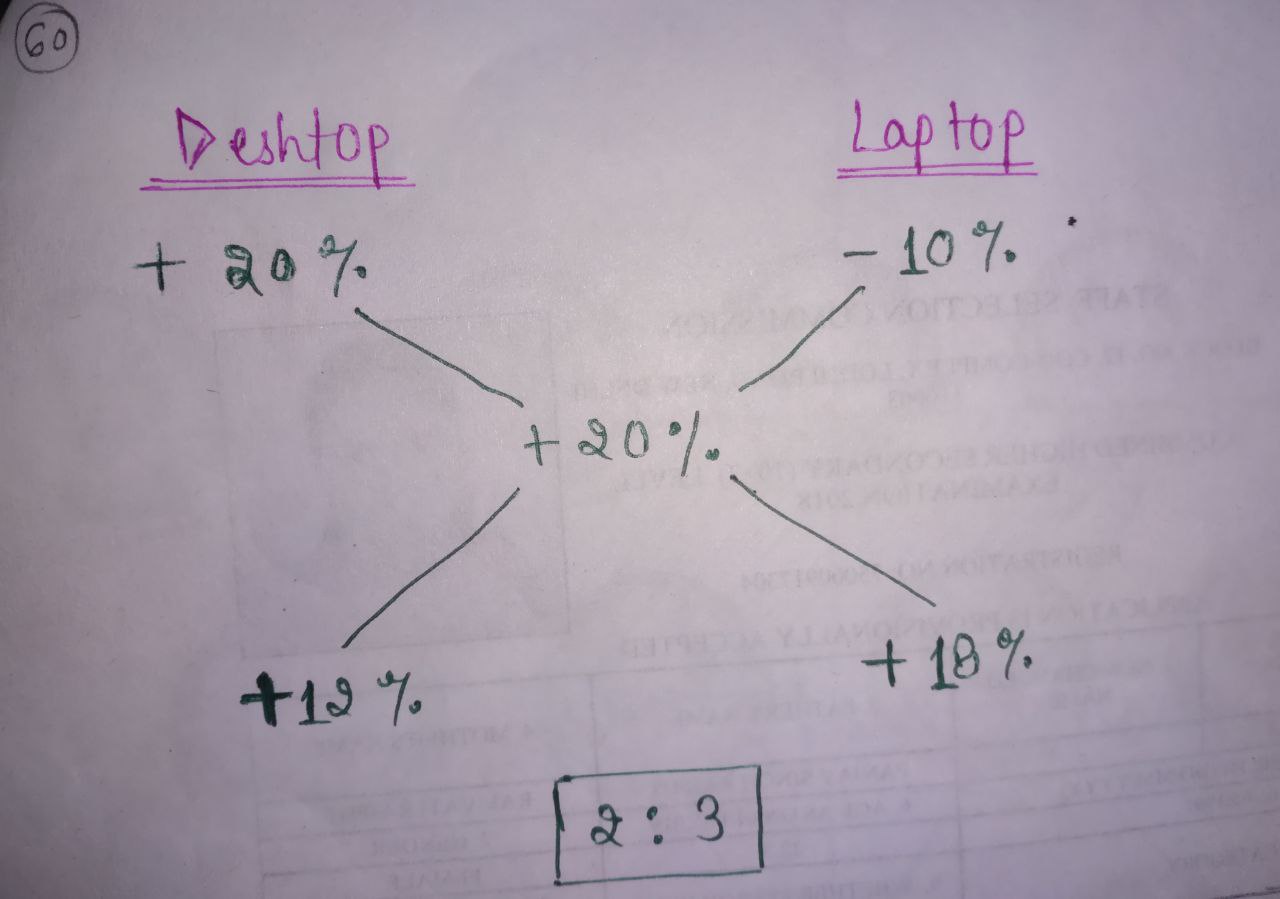
The ratio of cost price (purchase price) $ = 2 : 3 $
$\therefore$ The desktop purchase price $ = \frac{2}{5} \times 50000 = ₹ 20000.$
Correct Answer$: 20000$