We can draw the diagram for better visualization.
Let the distance from $A$ to $B$ be $\text{D}\; \text{km}.$
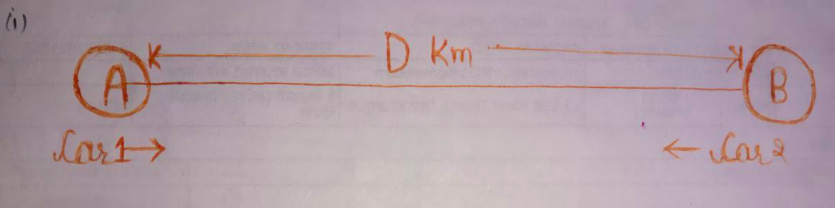
Let they meet at point $C.$
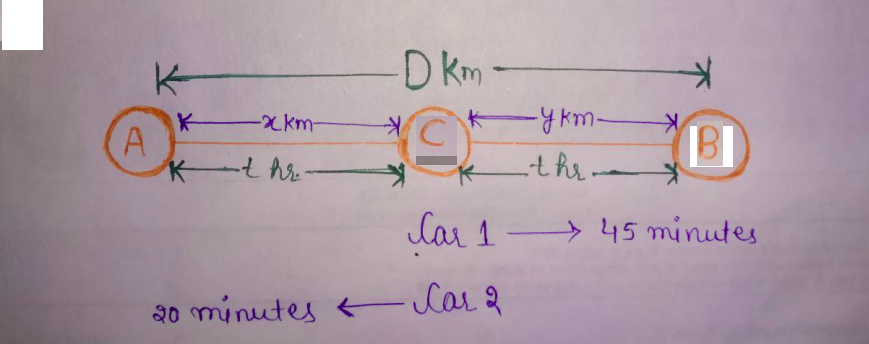
Let the speed of car $2$ be $\text{S} \; \text{km/hr}.$
We know that, $\boxed{\text{Speed}= \frac{\text{Distance}}{\text{Time}}}$
- For car $1: \text{t} = \frac{x}{60} \quad \longrightarrow (1)$
- For car $2: \text{t} = \frac{y}{\text{S}} \quad \longrightarrow (2)$
After meeting.
For car $1: \frac{45}{60} = \frac{y}{60}$
$\Rightarrow \boxed{y= 45 \; \text{km}}$
For car$2: \frac{20}{60} = \frac{x}{\text{S}}$
$\Rightarrow \boxed{ \frac{x}{\text{S}} = \frac{1}{3}} \quad \longrightarrow (3)$
Divide equation $(2)$ by equation $(1).$
$\Rightarrow \frac{t}{t} = \dfrac{\frac{y}{\text{S}}} {\frac{x}{60}}$
$\Rightarrow \left( \frac{y}{\text{S}} \right) \times \left( \frac{60}{x} \right) = 1$
$\Rightarrow \left( \frac{45}{\text{S}} \right) \times \left( \frac{60}{\frac{\text{S}}{3}} \right) = 1 \quad [\because \text{ From equation (3)}]$
$\Rightarrow \frac{\text{S}^{2}}{3} = 45 \times 60 $
$ \Rightarrow \text{S}^{2} = 180 \times 45$
$ \Rightarrow \text{S}^{2} = 8100$
$\Rightarrow \boxed{\text{S} = 90 \; \text{km/hr}}$
$\therefore$ The speed of car $2$ is $90 \; \text{km/hr}.$
$\textbf{Short Method:}$
We know that , $\text{ratio of speeds} = \sqrt{ \text{Inverse ratio of time taken}}$
So, speed of car $1:$ speed of car $2 = \sqrt{20:45} = \sqrt{4:9} = 2:3$
So, the speed of car $2 = 60 \times \frac{3}{2} = 90 \; \text{km/hr}.$
Correct Answer$:\text{A}$