Given that, a circle is inscribed in a rhombus with diagonal $12 \; \text{cm}$ and $16 \; \text{cm}.$
First, we can draw the figure.
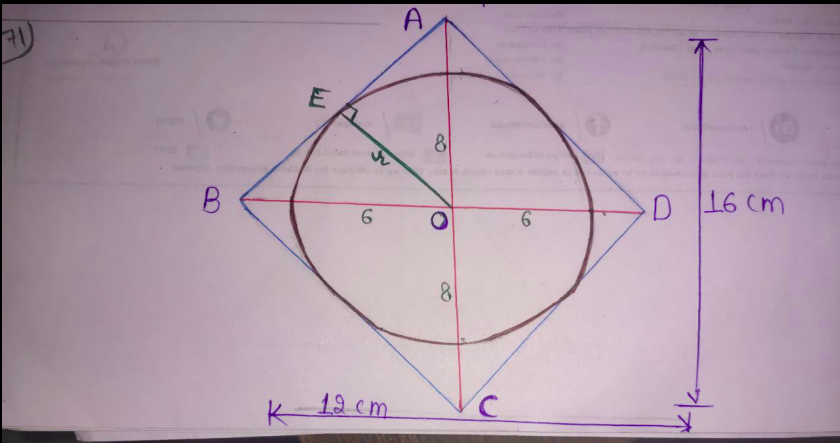
Let $\text{O}$ be the point of intersection of the diagonals of the rhombus and the center of the circle also.
Then, $\text{OE} \perp \text{AB}$
Let the radius of the circle $ = \text{OE} = r \; \text{cm}.$
Applying the pythagoras theorem to the $\triangle \text{AOB},$ we get.
$(\text{AB})^{2} = (\text{AO})^{2} + (\text{OB})^{2}$
$ \Rightarrow (\text{AB})^{2} = 8^{2} + 6^{2} $
$ \Rightarrow (\text{AB})^{2} = 64 + 36 = 100$
$ \Rightarrow \text{AB} = \sqrt{100} $
$ \Rightarrow \boxed{\text{AB} = 10 \; \text{cm}} $
Now, on considering the $\triangle \text{AOD},$ we can calculate its area in two ways.
Using hypotenuse $\text{AB}$ as the base, or using $\text{OB}$ as the base. The area will remain the same.
So, $\frac{1}{2} \times \text{AB} \times \text{OE} = \frac{1}{2} \times \text{OB} \times \text{OA}$
$ \Rightarrow 10 \times r = 6 \times 8 $
$ \Rightarrow r = \frac{24}{5} $
$ \Rightarrow \boxed{r = 4.8 \; \text{cm}}$
Now, the area of the circle $ = \pi r^{2} = \pi \times (4.8)^{2} = 23.04 \pi \; \text{cm}^{2}$
And the area of rhombus $ = \dfrac{1}{2} \times (\text{Product of the diagonal lengths}) = \frac{1}{2} \times 12 \times 16 = 96 \; \text{cm}^{2}$
$\therefore$ The ratio of the area of the circle to the area of rhombus $ = \dfrac{23.04 \pi \; \text{cm}^{2}}{96 \; \text{cm}^{2}} = \dfrac{6 \pi}{25}.$
Correct Answer $: \text{B}$