Given that, a chord length $5 \; \text{cm}$ subtends an angle of $60^{\circ}$ at the centre of a circle.
Let the radius of a circle be $`r\text{’} \; \text {cm}.$
So, $\boxed{OA = OB = OC = r}$
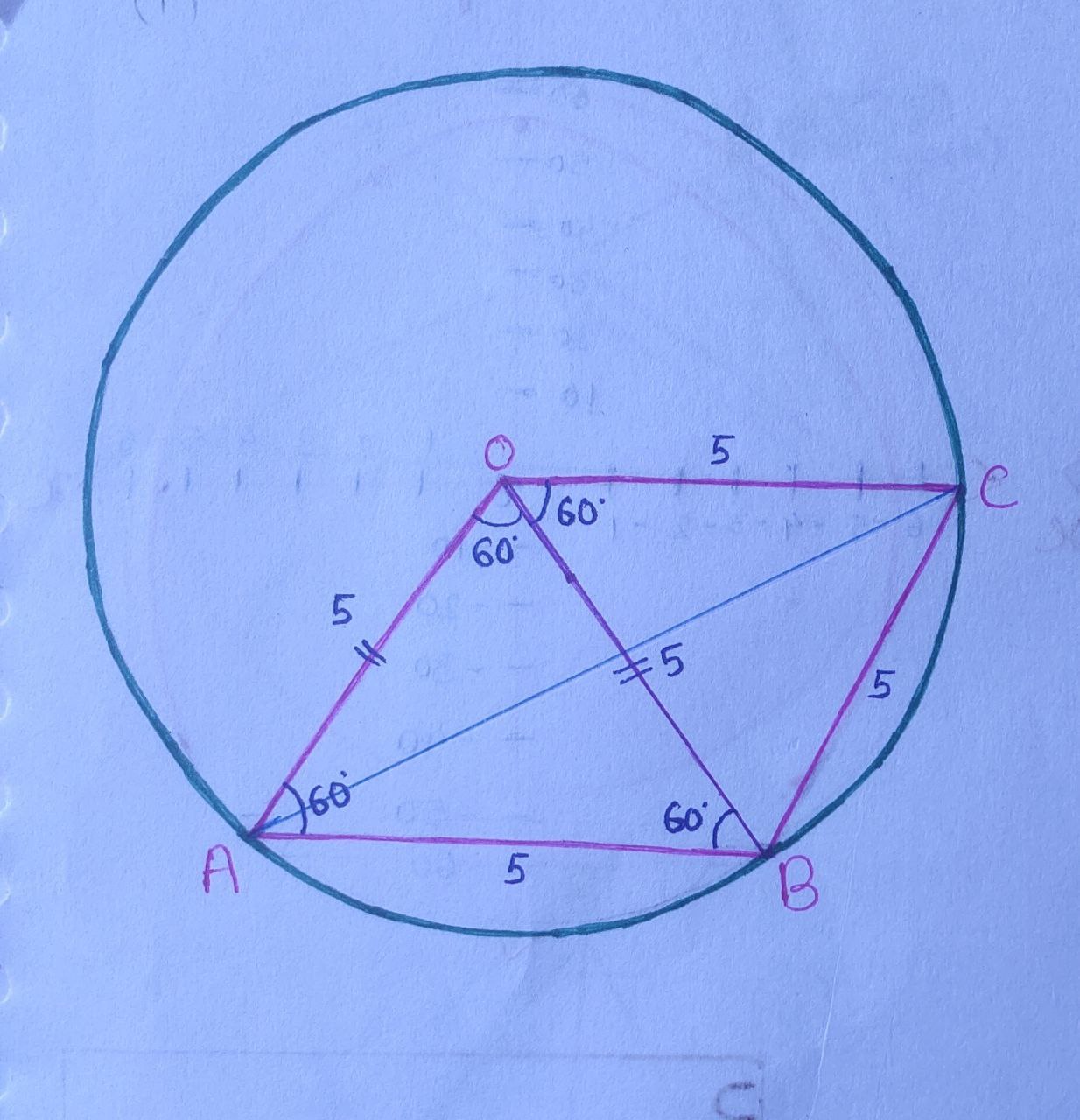
In $\triangle OAB,$ two sides are equal $(OA = OB = r).$
So, $\angle A = \angle B = 60^{\circ}$
Thus, $\triangle ABC$ is an equilateral triangle.
$OABC$ is a rhombus.
Area of rhombus $= \frac{d_{1} \times d_{2}}{2} \; \text{sq. units},$ where $d_{1}, d_{2}$ are the diagonal of the rhombus.
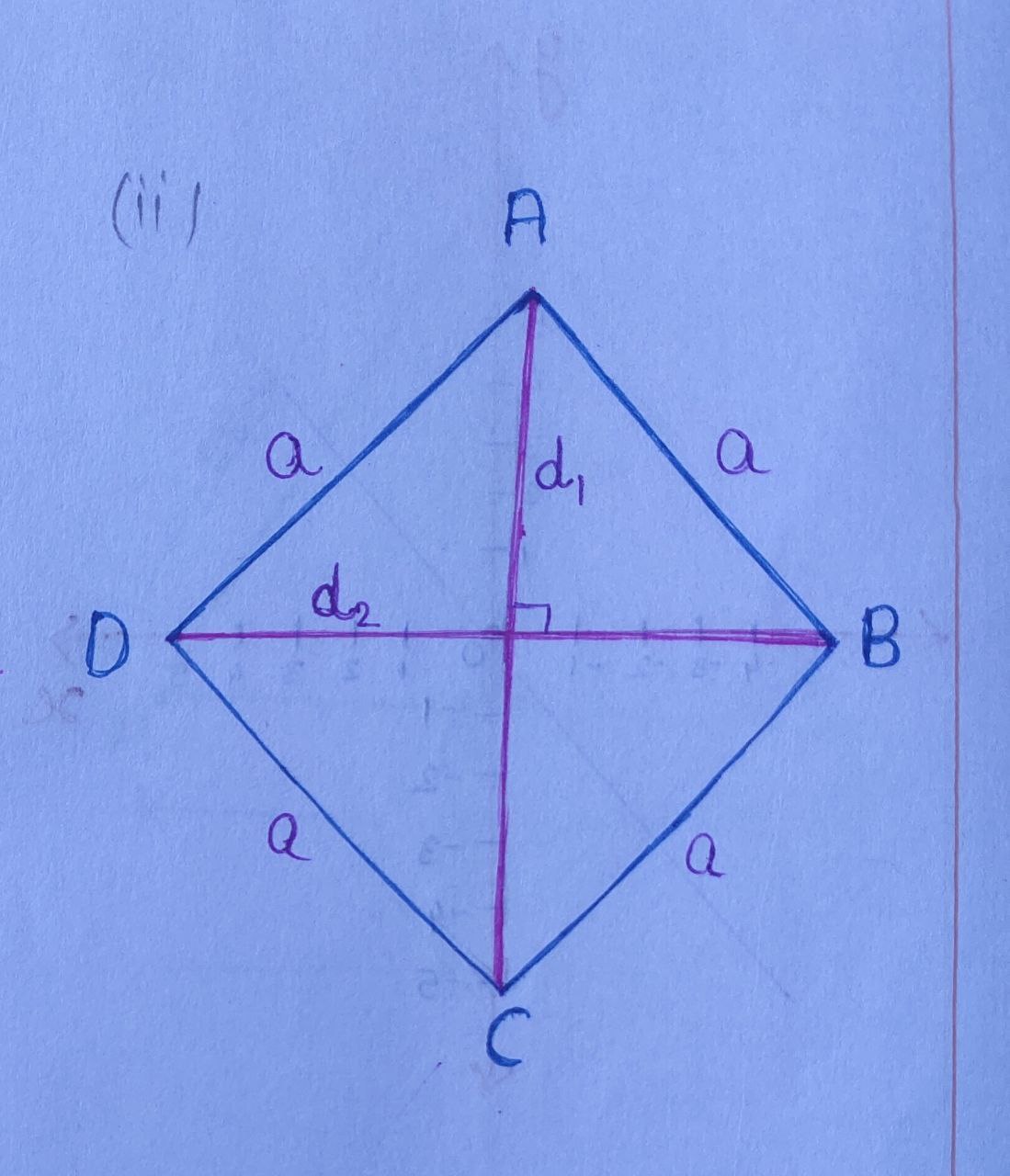
Diagonals are perpendicular, to each other. $ \boxed{d^{2}_{1} + d^{2}_{2} = 4a^{2}} $
So, $ (OB)^{2} + (AC)^{2} = 4r^{2} $
$ \Rightarrow (5)^{2} + (AC)^{2} = 4(5)^{2} $
$ \Rightarrow 25 + (AC)^{2} = 100 $
$ \Rightarrow (AC)^{2} = 75 $
$ \Rightarrow AC = \sqrt{75} = \sqrt{25 \times 3} $
$ \Rightarrow AC = 5 \sqrt{3} \; \text{cm} $
$\therefore$ The length of a chord that subtends an angle of $120^{\circ}$ at the center of the circle is $5 \sqrt{3} \; \text{cm}.$
Correct Answer $:\text{C}$