Let the volume of liquids in Bottle $1$ and Bottle $2$ be $x$ liter and $y$ liter respectively.
Now, $\dfrac{(\frac{7}{9})x+(\frac{9}{13})y}{(\frac{2}{9})x+(\frac{4}{13})y}= \dfrac{3}{1}$
$\Rightarrow (\frac{7}{9})x+(\frac{9}{13})y=3\left[(\frac{2}{9})x+(\frac{4}{13})y\right]$
$\Rightarrow \frac{7x}{9}+\frac{9y}{13}=\frac{6x}{9}+\frac{12y}{13}$
$\Rightarrow \frac{7x}{9}-\frac{6x}{9}=\frac{12y}{13}-\frac{9y}{13}$
$\Rightarrow \frac{7x-6x}{9}=\frac{12y-9y}{13}$
$\Rightarrow \frac{x}{9}=\frac{3y}{13}$
$\Rightarrow \frac{x}{y}=\frac{27}{13}$
$\therefore$ The Bottle $1$ and Bottle $2$ should be combined in the ratio of $x:y=27:13.$
$\textbf{Short Method:}$
We can solve this question using the allegation method.
Now,
- In Bottle $1$ concentration of milk $=\frac{7}{9}$
- In bottle $2$ concentration of milk $=\frac{9}{13}$
- In mixture concentration of milk $=\frac{3}{4}$
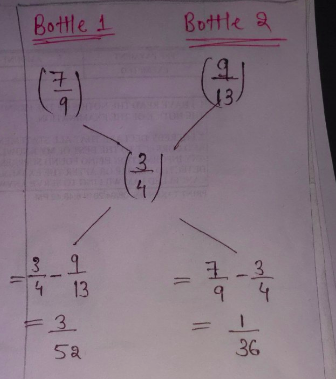
$\therefore$ The required ratio $=\dfrac{\frac{3}{52}}{\frac{1}{36}}=\frac{3}{52}\times{\frac{36}{1}}=\frac{27}{13}.$
$$\textbf{(OR)}$$
- In bottle $1$ concentration of water $=\frac{2}{9}$
- In bottle $2$ concentration of water $=\frac{4}{13}$
- In mixture concentration of water $=\frac{1}{4}$
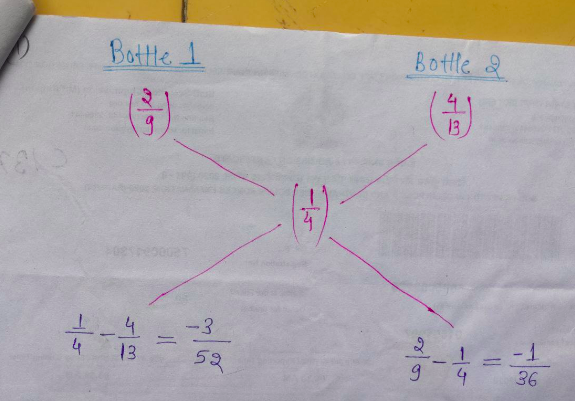
$\therefore$ The required ratio $=\dfrac{\frac{-3}{52}}{\frac{-1}{36}}=\frac{3}{52}\times{\frac{36}{1}}=\frac{27}{13}.$
Correct Answer $:\text{B}$