CAT 2017 Set-2 | Question: 70

Question

Arun drove from home to his hostel at $60$ miles per hour. While returning home he drove halfway along the same route at a speed of $25$ miles per hour and then took a bypass road which increased his driving distance by $5$ miles, but allowed him to drive at $50$ miles per hour along this bypass road. If his return journey took $30$ minutes more than his onward journey, then the total distance traveled by him is

• A. $55$ miles
• B. $60$ miles
• C. $65$ miles
• D. $70$ miles

Answer 1

Let the distance from his home to his hostel be $D$ miles.

 We know that, $\text{Time} = \dfrac{\text{Distance}}{\text{Speed}}$

Time has taken on his onward journey  $T_{\text{onward}} = \frac{D}{60}$  hours

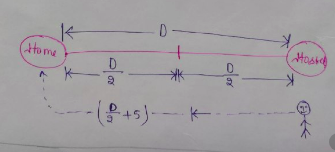
Time taken on his return journey  $T_{\text{return}} = \left[\frac{\left(\frac{D}{2}\right)}{25}+\frac{\left(\frac{D}{2}+5\right)}{50}\right]$  hours

His return journey took $30$ minutes more than his onward journey.

That means,  $T_{\text{return}} = T_{\text{onward}} + 30$ minutes

$\Rightarrow \frac{\frac{D}{2}}{25}+\frac{\frac{D}{2}+5}{50} = \frac{D}{60}+\frac{30}{60}$

$\Rightarrow \frac{D}{50}+\frac{D+10}{100} = \frac{D+30}{60}$

$\Rightarrow \frac{2D+D+10}{100} = \frac{D+30}{60}$

$\Rightarrow 3(3D+10) = 5(D+30)$

$\Rightarrow 9D+30 = 5D+150$

$\Rightarrow 4D = 120$

$\Rightarrow \boxed{D = 30\;\text{miles}}$

$\therefore$  The total distance traveled by him $ = D+\frac{D}{2}+\frac{D}{2}+5 = D+15+15+5 = 65$ miles.

Correct Answer $:\text{C}$