Given that, the straight line $ 3x + 5y – 45 = 0 \quad \longrightarrow (1) $
We know that,
- In $ x – \text{axis}, y = 0 $
- In $ y – \text{axis}, x = 0 $
Now, put $x=0$ in the equation $(1),$ we get
$ 3(0) + 5y – 45 = 0 $
$ \Rightarrow 5y – 45 = 0 $
$ \Rightarrow \boxed{y=9}$
We get, the coordinate $\boxed{(x,y) = (0,9)}$
And, put $y=0$ in the equation $(1),$ we get
$ 3x + 5(0) – 45 = 0 $
$ \Rightarrow 3x – 45 = 0 $
$ \Rightarrow \boxed{x=15} $
We get, the coordinate $\boxed{(x,y) = (15,0)}$
Now, we can draw the diagram as follow :
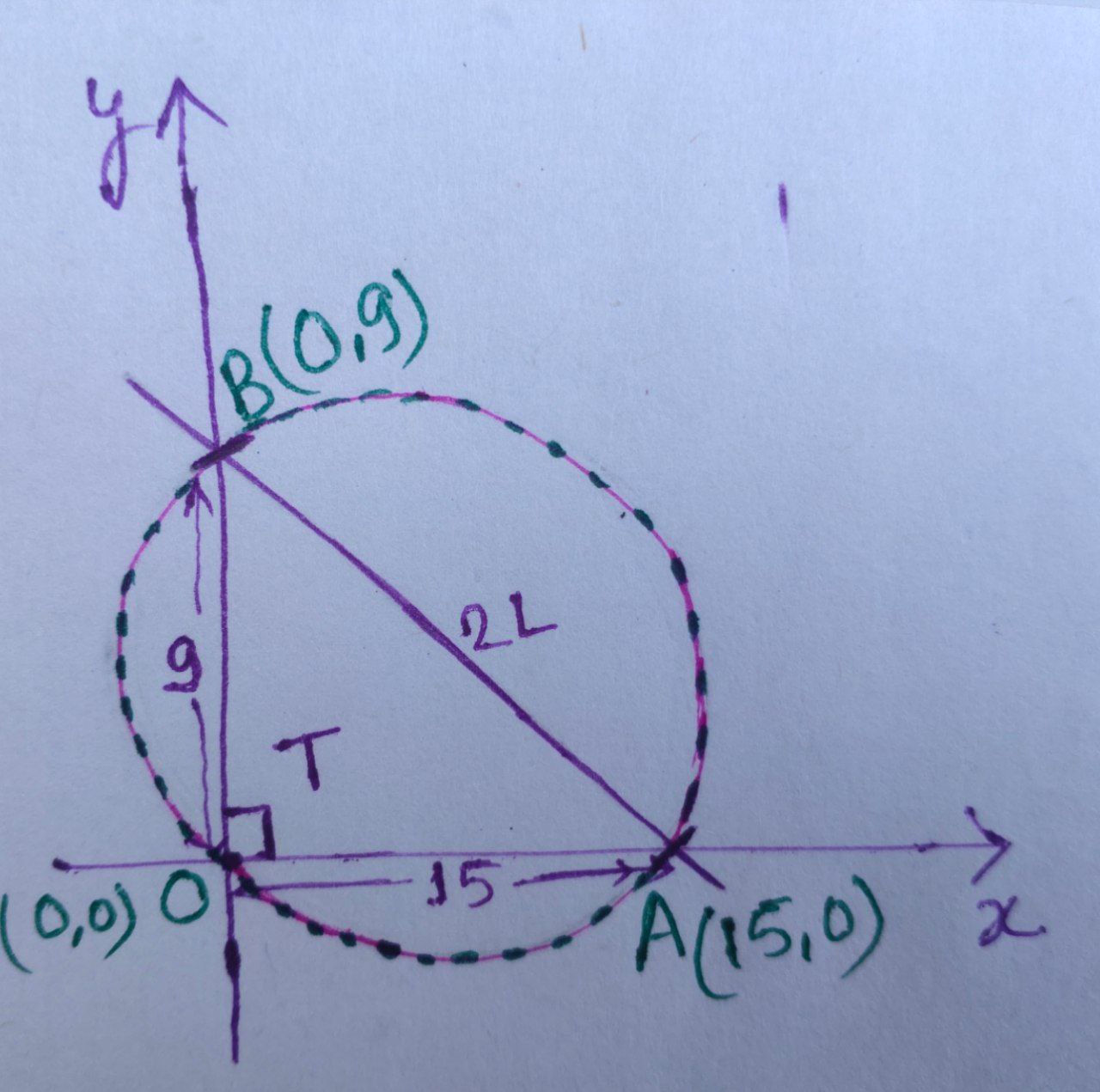
We have$, \triangle \text{AOB}$ is right angle triangle, then we can apply the Pythagoras’ theorem :
$ \boxed{ \text{Hypotenuse}^{2} = \text{Perpendicular}^{2} + \text{Base}^{2}} $
Now, $ \text{(AB)}^{2} = \text{(OA)}^{2} + \text{(OB)}^{2} $
$ \Rightarrow (2 \text{L})^{2} = 15^{2} + 9^{2} $
$ \Rightarrow 4 \text{L}^{2} = 225 +81 $
$ \Rightarrow 4 \text{L}^{2} = 306 $
$ \Rightarrow \text{L}^{2} = \frac{306}{4} = 76 \cdot 5 $
$ \Rightarrow \text{L} = \sqrt{76 \cdot5} = 8 \cdot746 \approx 9.$
$\therefore$ The radius of circumcircle $ \text{L} = 9 $ units.
$\textbf{PS:}$ In a right-angle $\triangle \text{AOB},$ hypotenuse is the diameter of a circumcircle.
Correct Answer $:9$