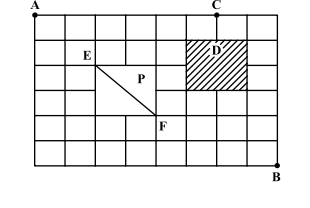
The answer provided in the previous post is right but the explanation is incorrect.
The shortest path will be A → E → F→ B. Because the entire map is symmetric but the diagonal creates a new shorter path from E→ F. Diagonal is shorter than the sum of its perpendicular and base (Pythagoras Theorem’s Corollary).
Now to go from A to E, we have to travel right two times and travel downwards two times. So, we could for example, take R, D, R and D or we could take R, R, D, D. So how many such arrangements are possible ?? Lets list them down :-
R R D D, D D R R, R D R D, D R D R, R D D R, D R R D – Six arrangements possible
So the questions is how many permutations/arrangements of these four roads (R R D D) is possible given two of them are repeating twice.
It is : $\large \frac{^{4} P_{4}}{2!*2!} = \frac{4!}{2! * 2!} = 6$
Similarly, for F to B, we have to take four rights and two downs (R R R R D D). So the number of arrangements of these six roads, one which repeats twice and the other repeats four times is :
$\large \frac{^{6} P_{6}}{4!*2!} = \frac{6!}{4! * 2!} = 15$
Therefore, the total number of ways are : $\large 6 *15 = 90$.