Assuming, Initially $A's$ speed is $3x\hspace{0.1cm}km/hr$ & $B's$ speed is $x\hspace{0.1cm}km/hr$.
So, in a certain amount of time, $A$ is travelling $\dfrac{3}{4}^{th} $ distance of circle, whereas in that time $B$ is travelling only $\dfrac{1}{4}^{th} $ distance of circle.
let's see the pictorial representation of the events.
I'm going to divide the circle into $4$ equal halves,as if in a certain period of time $A$ is covering $3$ units of distance & in the same amount of time $B$ is covering $1$ unit of distance. then the circle should be divided into $(3+1)=4$ equal halves.
$A$ & $B$ is starting from $M_0$ & Both are running opposite direction of each other & as $A's$ speed is $3x\hspace{0.1cm} km/hr$ & $B's$ speed is $x km/hr$, $A$ will cover $3$ units, whereas $B$ will cover $1$ units & both will meet at $M_1$ point .
Now $A$ & $B's$ speed will be reversed as per the criterion. $A's$ speed will be $x\hspace{0.1cm}km/hr$ & $B's$ speed will be $3x\hspace{0.1cm}km/hr$
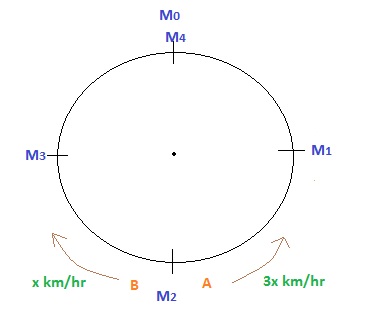
After meeting this point , $A's$ speed will be $3x\hspace{0.1cm}km/hr$ & $B's$ speed will be $x\hspace{0.1cm}km/hr$
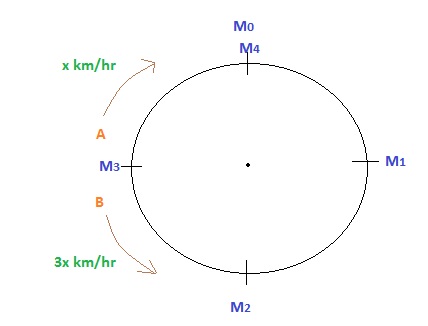
After meeting this point , $A's$ speed will be $x\hspace{0.1cm}km/hr$ & $B's$ speed will be $3x\hspace{0.1cm}km/hr$
$\text{And, Finally, they'll meet at}$ $M_4$.
Now, the question ask us to find the shortest distance between $M_1$ & $M_2$
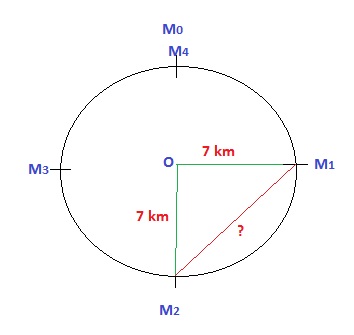
Applying Pythagoras Theorem,
$(OM_{1})^{2}+(OM_{2})^{2}= (M_{1}M_{2})^2$
Or, $7^2+7^2 =(M_{1}M_{2})^2$
Or, $98 =(M_{1}M_{2})^2$
Or, $\sqrt{98} =(M_{1}M_{2})$
Or, $(M_{1}M_{2})= 7\sqrt{2}$
$\color{green}{\text{∴ The shortest distance between}}$ $\color{red}{M_{1}}$ $\color{green}{and}$ $\color{red}{M_{2}}$ $\color{green}{is}$ $\color{orange}{7\sqrt{2}\hspace{0.1cm}km}$