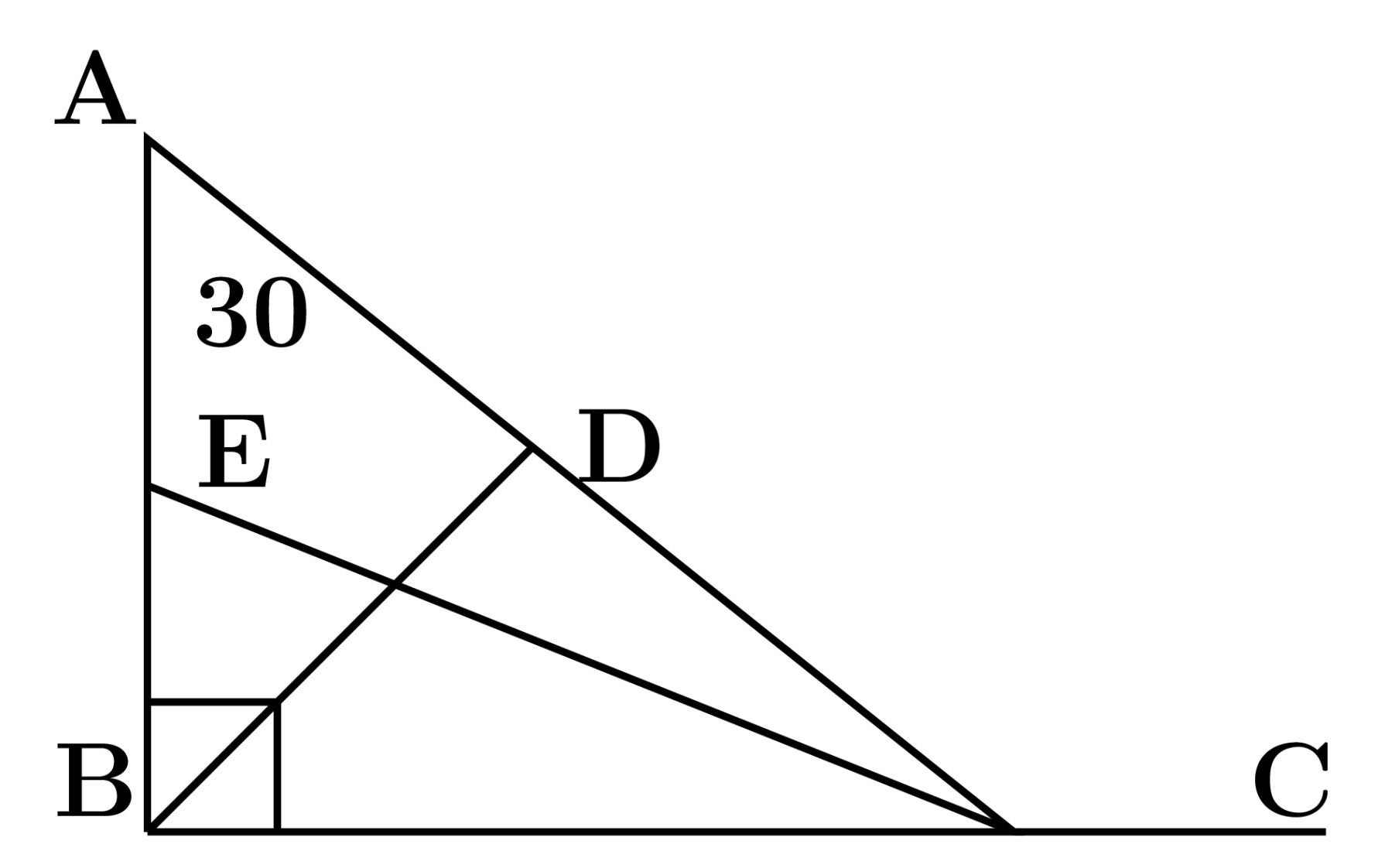
$AB\perp BC$ & $BD \perp AC$
∴$\measuredangle ABC = 90^{\circ} $ & $\measuredangle BDA = \measuredangle BDC = 90^{\circ}$
Now, $\angle BAC = 30^{\circ}$
∴$\measuredangle ACB = 180^{\circ} - (90^{\circ}+30^{\circ})$
$\measuredangle ACB = 180^{\circ} - 120^{\circ}$
$\measuredangle ACB = 60^{\circ} $
Given that $CE$ bisects $\angle C$
$∴ \measuredangle ECD = \dfrac{60^{\circ}}{2}= 30^{\circ} $
Then, $\measuredangle CED = 180^{\circ} - (90^{\circ}+30^{\circ}) = 60^{\circ}$