CAT 2001 | Question: 40

Question

Based on the figure below, what is the value of $x,$ if $y = 10?$

• A. $0$
• B. $11$
• C. $12$
• D. None of these

 

Answer 1

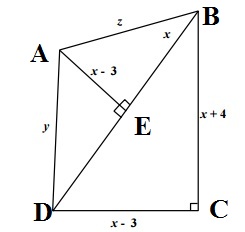
We can find the value of $x$ by checking with the given options.

Consider $\triangle ADE$ using Pythagoras Theorem and put $x=11$

$y^2=(x-3)^2+(DE)^2$, put $y=10$ and after solving we get $DE=6$.

now consider $\triangle BCD$ using Pythagoras theorem $(BD)^2=(BC)^2+(DC)^2$

$\implies (11+6)^2=15^2+8^2$

$\implies 289=289$ which satisfies the condition.

Option (B) is correct.