Let’s draw the diagram.
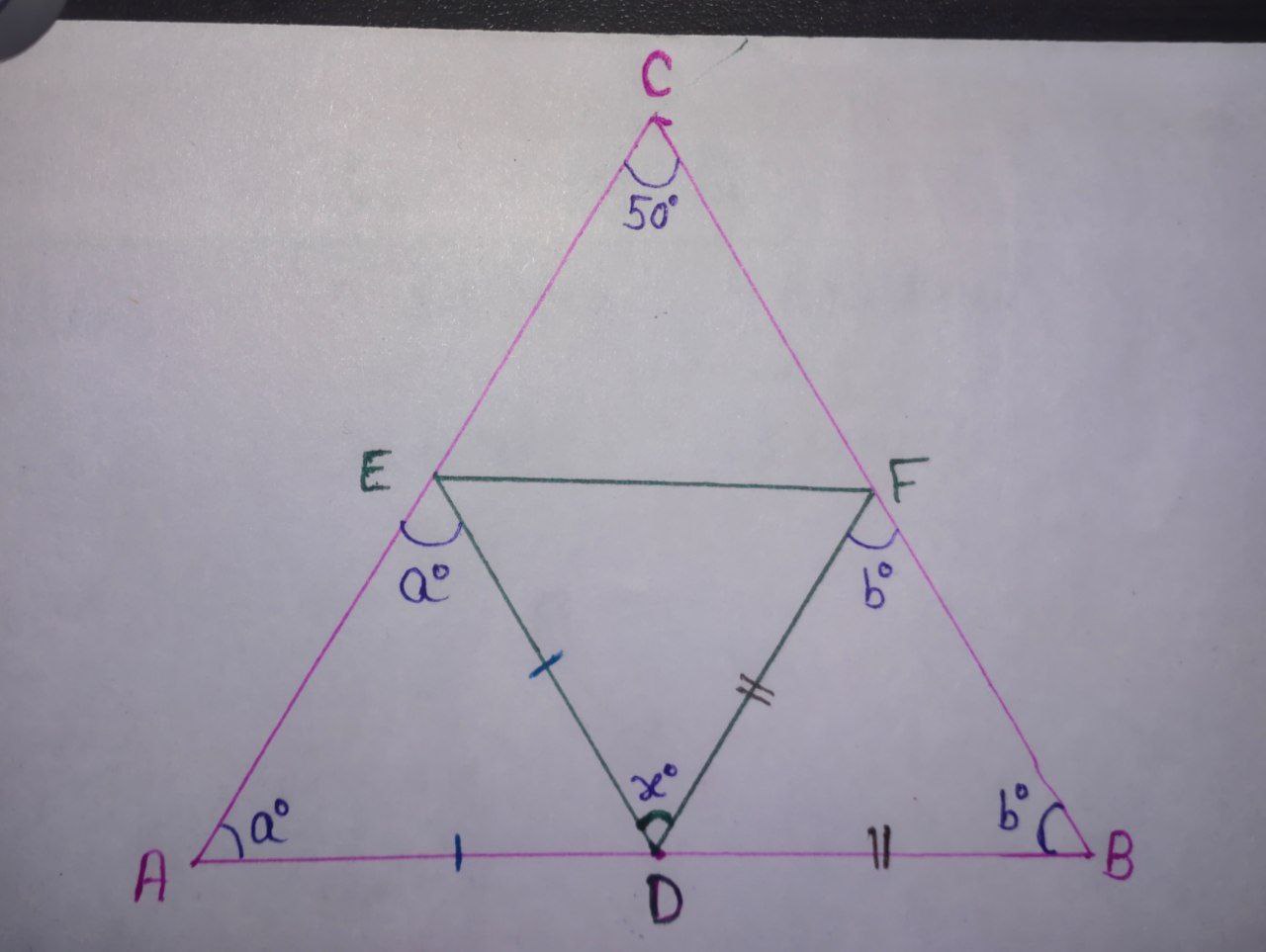
Let, the $\angle \text{DAE} = \angle \text{AED} = a^{\circ},$ and $\angle \text{DFB} = \angle \text{FBD} = b^{\circ},$ and $\angle \text{FDE}=x^{\circ}.$
Now,
- $\angle \text{ADE} = 180^{\circ} – 2x^{\circ}$
- $\angle \text{BDF} = 180^{\circ} – 2y^{\circ}$
We know that, angle on straight line equal to $180^{\circ}.$
So, $180–2a+x+180-2b=180$
$\Rightarrow x-2a-2b+180=0$
$\Rightarrow x=2a+2b-180 \; \longrightarrow (1) $
In $\triangle \text{ABC}, a+b+50=180 \quad [\because \text{Sum of the angles of triangle} = 180^{\circ}]$
$\Rightarrow a+b=130$
Put the value of $a+b$ in equation $(1).$
$\Rightarrow x=2(a+b)-180$
$\Rightarrow x=2(130)-180$
$\Rightarrow x=260-180$
$\Rightarrow \boxed{x=80^{\circ}}$
$\therefore$ The $\angle \text{FDE},$ in degree, is equal to $80^{\circ}.$
Correct Answer $:\text{C}$