Let’s draw the track.
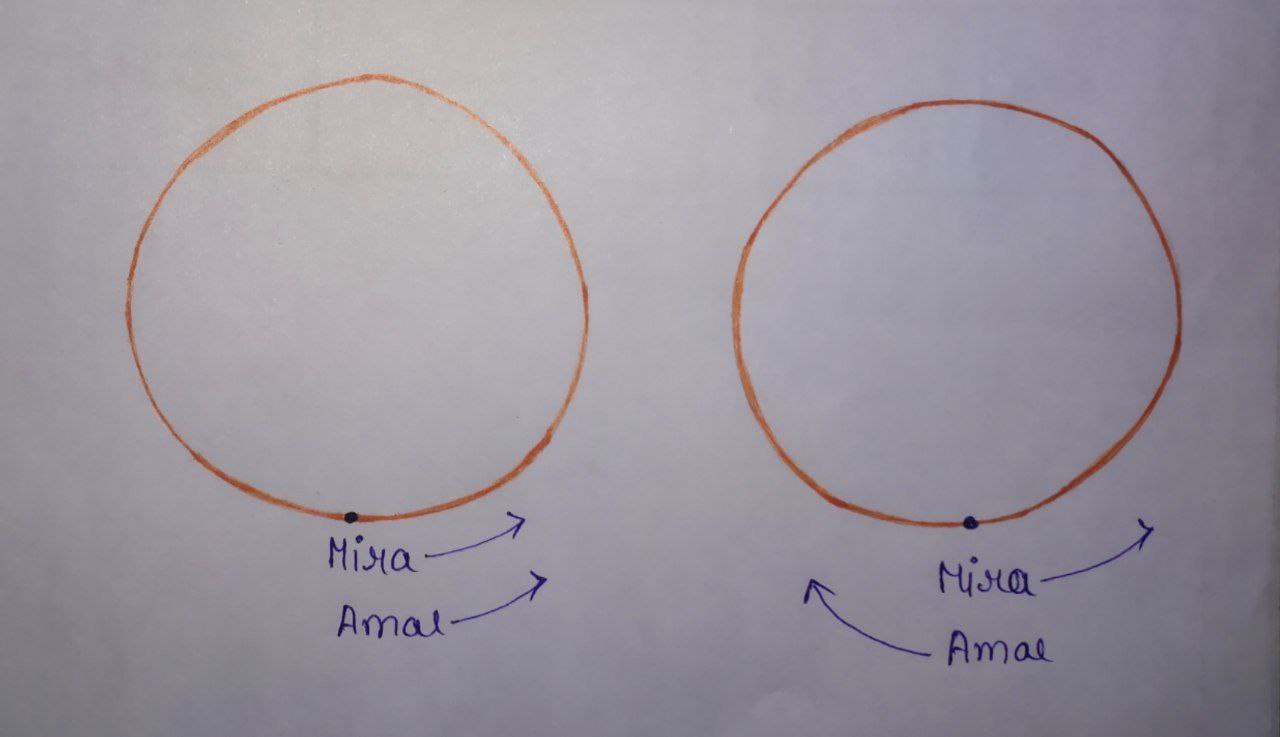
Let the length (circumference) of the circular track be $\text{L}$ km.
Let the distance traveled by Mira in $1$ minute be $\text{M}$ km, and the distance traveled by Amal in $1$ minute be $\text{A}$ km.
Now, $45 \; \text{A} = 45 \; \text{M} + 3 \; \text{L}$
$\Rightarrow 45 \; \text{A} - 45 \; \text{M} = 3 \;\text{L} \; \longrightarrow(1)$
And $\text{3A} + \text{3M} = \text{L} \quad \longrightarrow(2)$
From equation $(1)$ and $(2).$
$\require{cancel} \begin{array}{} 45 \; \text{A} - 45 \; \text{M} = 3 \; \text{L} \\ (\text{3A} + \text{3M} = \text{L}) \times 15 \\\hline \cancel{45 \; \text{A}} - 45 \; \text{M} = 3 \; \text{L} \\ \cancel{45 \; \text{A}} + 45 \; \text{M} = 15 \; \text{L} \\ \;– \qquad \quad – \qquad \quad– \\\hline \qquad \quad -90 \; \text{M} = -12 \; \text{L} \end{array}$
$\Rightarrow \text{M} = \frac{12 \; \text{L}}{90}$
$\Rightarrow \boxed{\text{M} = \frac{2 \; \text{L}}{15}}$
Now,
- $1 \; \text{minute} \; \longrightarrow \frac{2 \; \text{L}}{15}$
- $60 \; \text{minute} \; \longrightarrow \frac{2 \; \text{L}}{15} \times 60$
- $1 \; \text{hour} \; \longrightarrow \; 8 \; \text{L}$
$\therefore$ The number of rounds Mira walks in one hour is $8\;\text{rounds}.$
Correct Answer $:8$