Let the length of train $\text{A}$ be $x \; \text{m},$ and the length of train $\text{B}$ be $y \; \text{m}.$
Let the speed of train $\text{A}$ be $5s \; \text{m/sec},$ and the speed of train $\text{B}$ be $3s \; \text{m/sec}.$
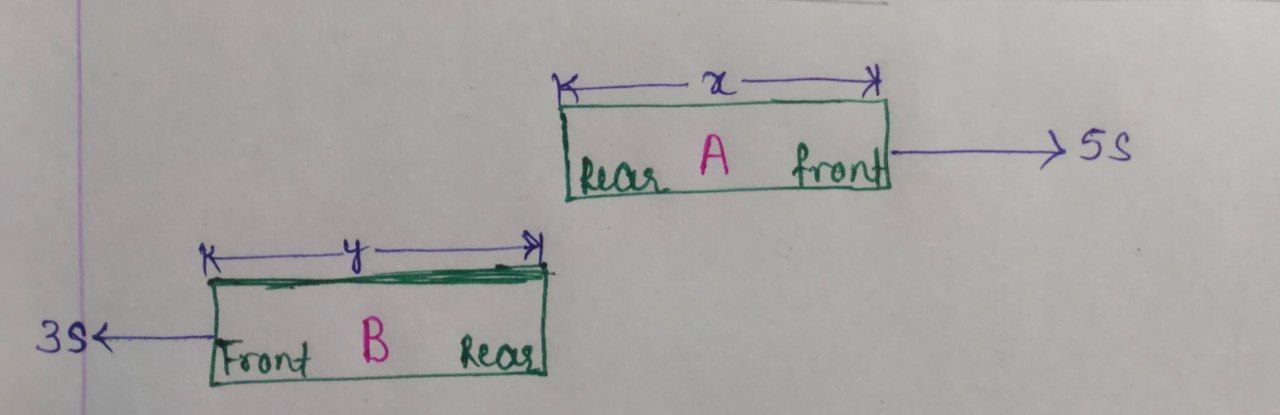
Let’s draw the diagram for a better understanding.
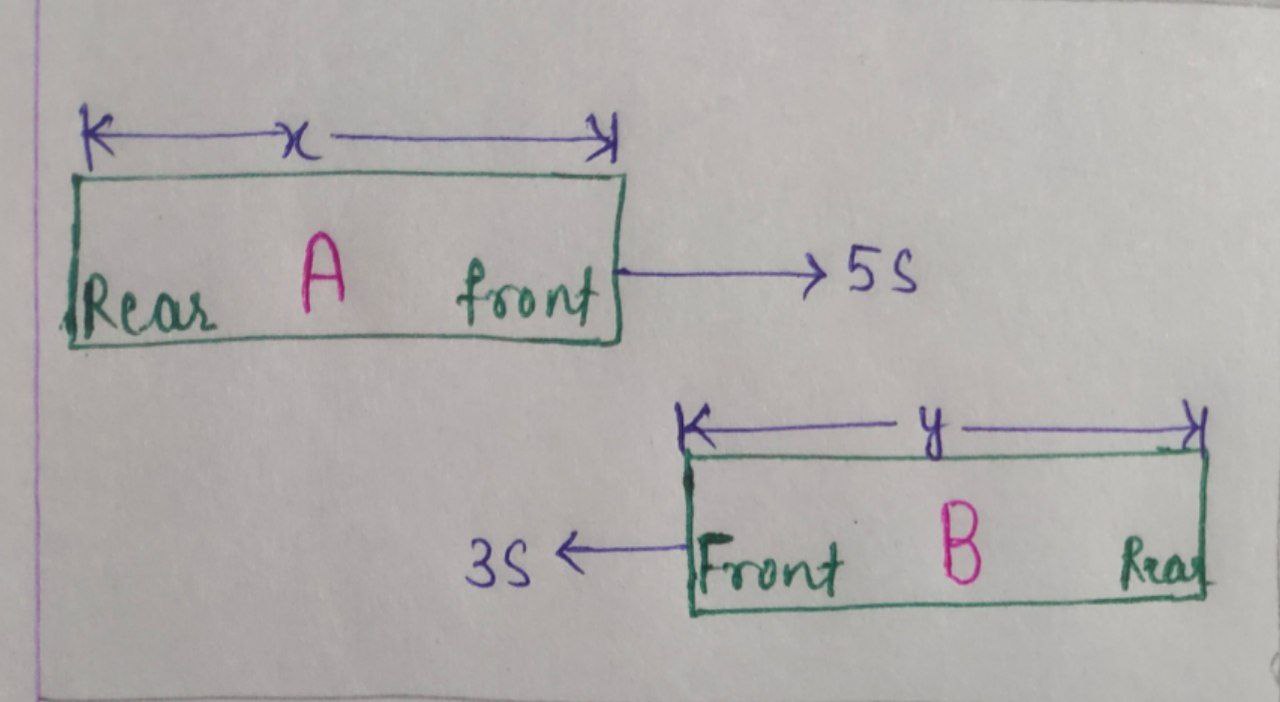
The front end of $\text{A}$ crossed the rear end of $\text{B 46}$ seconds after the front ends of the trains had crossed each other.
Here, $ y = 46 \times 8s \quad \longrightarrow (1)$
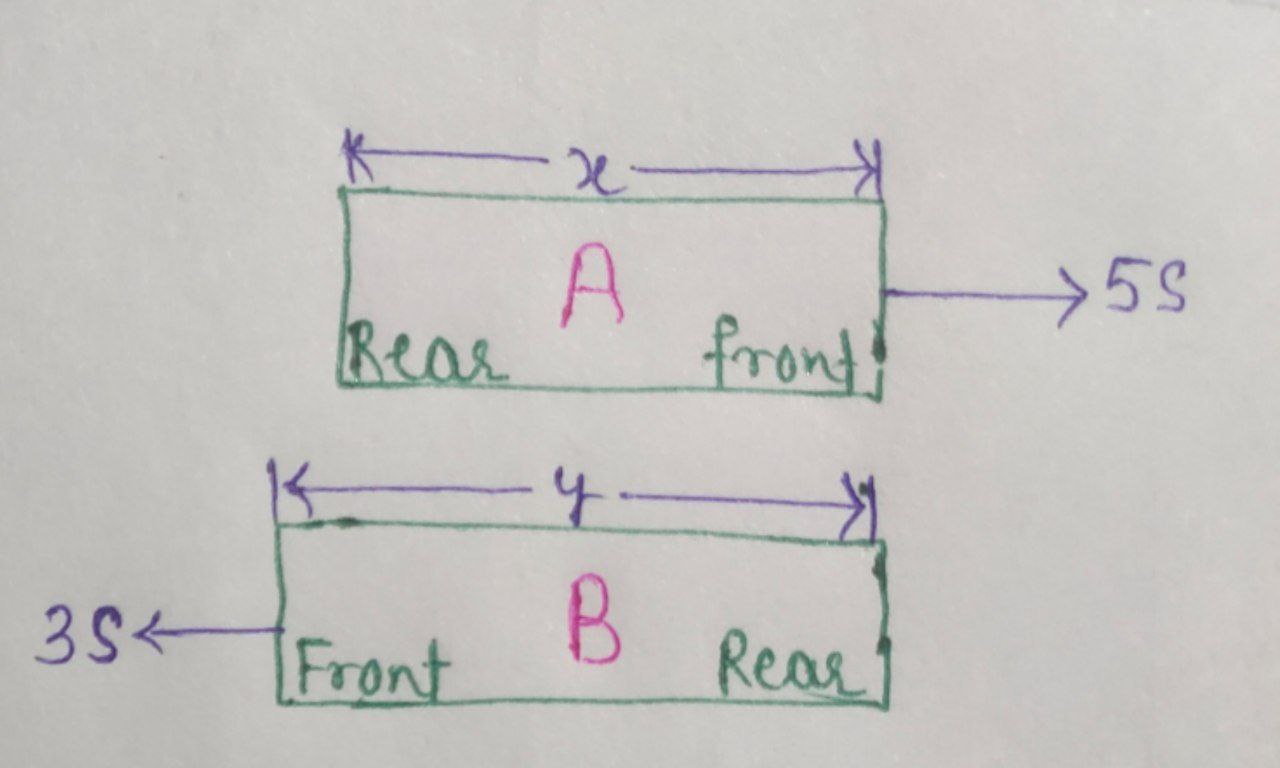
It took another $69$ seconds for the rear ends of the trains to cross each other.
Here, $ x = 69 \times 8s \quad \longrightarrow (2)$
Divide equation $(2)$ by equation $(1).$
$\Rightarrow \frac{x}{y} = \frac{ 69 \times 8s}{46 \times 8s}$
$ \Rightarrow \frac{x}{y} = \frac{3}{2}$
$\therefore$ The ratio of length of train $\text{A}$ to that of train $\text{B} = x : y = 3 : 2.$
Correct Answer $: \text{C}$
$\textbf{PS:}\;\text{Important points:}$
- When two trains are going in the same direction, then their relative speed is the difference between the two speeds.
- When two trains are moving in the opposite direction, then their relative speed is the sum of the two speeds.
- When a train crosses a stationary man/ pole/ lamp post/ sign post- in all these cases, the object which the train crosses is stationary, and the distance traveled is the length of the train.
- When it crosses a platform/ bridge- in these cases, the object which the train crosses are stationary and the distance traveled is the length of the train and the length of the object.
- When two trains are moving in the same direction, then their speed will be subtracted.
- When two trains are moving in opposite directions, then their speed will be added.
- In both the above cases, the total distance is the sum of the length of both the trains.