Given that, $f(x) = \dfrac{x^{2} + 2x – 15}{x^{2} – 7x – 18}$
Now, if $f(x) < 0$
Then, $\dfrac{x^{2} + 2x – 15}{x^{2} – 7x – 18} < 0$
$ \Rightarrow \dfrac{x^{2} + 5x – 3x – 15}{x^{2} – 9x + 2x – 18} < 0$
$ \Rightarrow \dfrac{(x+5)(x-3)}{(x-9)(x+2)} < 0$
We can draw the number line.
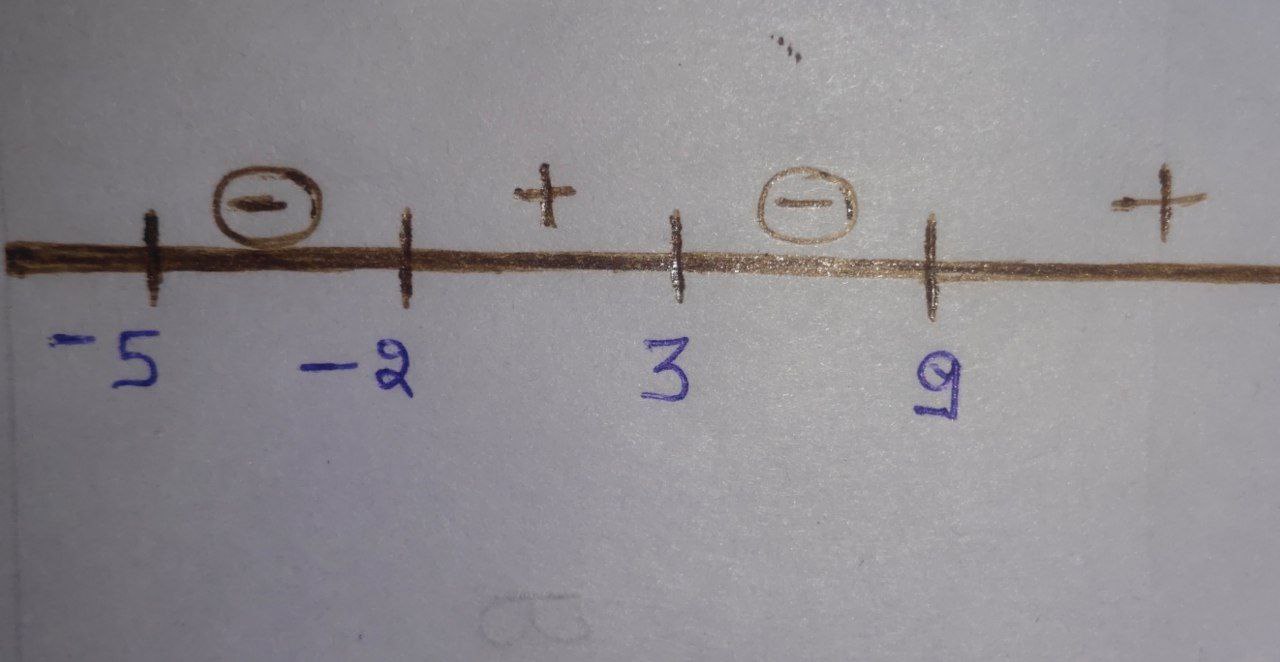
$x \in (-5, -2) \cup (3, 9)$
$ \boxed{-5 < x < -2 \; \text{(or)} \; 3 < x < 9}$
Correct Answer $:\text{C}$