Given that, diameter of a circle $ = 8 \; \text{inches},$ and $\angle \text{ABC} = 90^{\circ}, \text{BC} = 10 \; \text{inches.}$
Let’s draw the diagram.
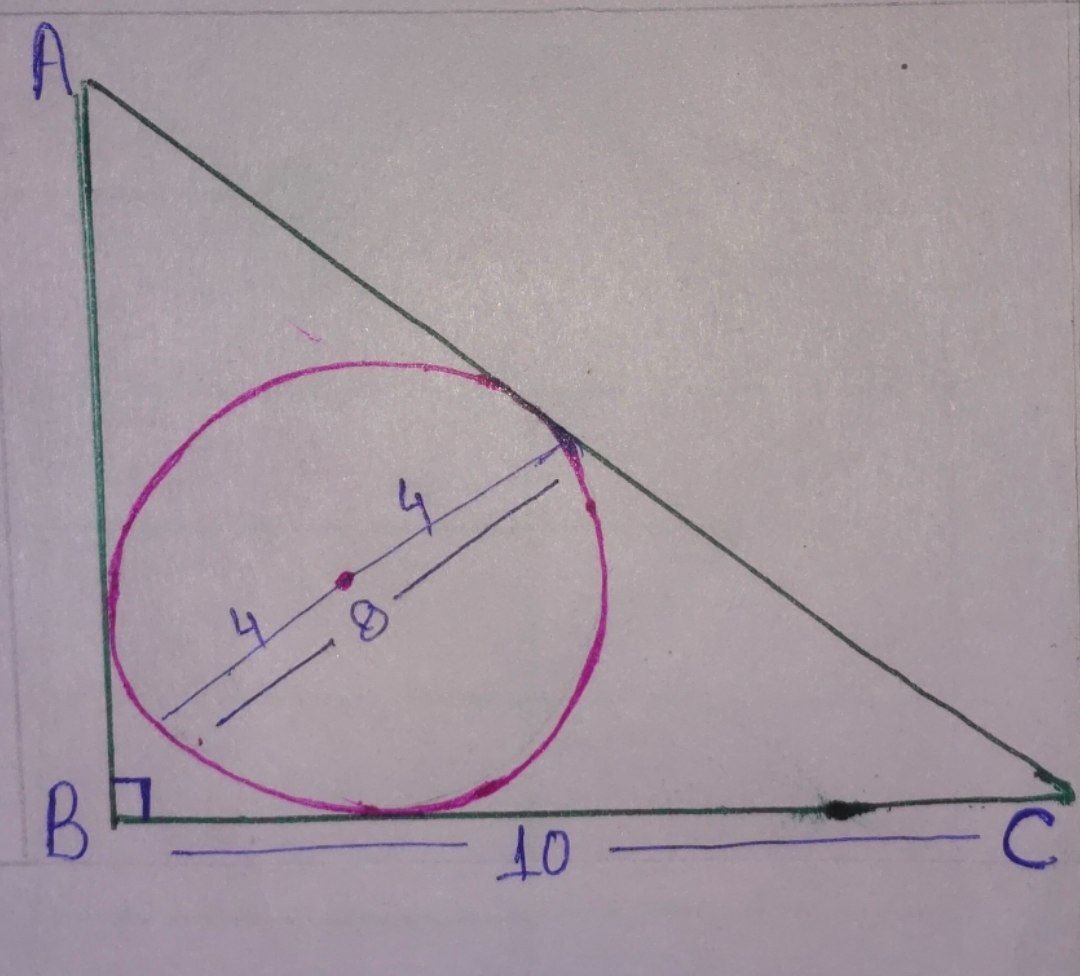
We know that, $\boxed {\text{Radius} = \frac{ \text{Perpendicular (AB) + Base (BC) – Hypotenuse (AC)}}{2}}$
$ \Rightarrow 4 = \frac{\text{AB + BC – AC}}{2}$
$ \Rightarrow 8 = \text{AB + 10 – AC}$
$ \Rightarrow \; – 2 = \text{AB – AC}$
$ \Rightarrow \boxed {\text{AB} = \text{AC – 2}}$
$\triangle \text{ABC}$ is a right-angle triangle, so we can apply the Pythagorean theorem.
$\text{(Hypotenuse)}^{2} = \text{(Perpendicular)}^{2} + \text{(Base)}^{2}$
$\Rightarrow \text{(AC)}^{2} = \text{(AB)}^{2} + \text{(BC)}^{2}$
$ \Rightarrow \text{(AC)}^{2} = \text{(AC – 2)}^{2} + (10)^{2}$
$\Rightarrow \text{(AC)}^{2} = \text{(AC)}^{2} + 4 – \text{4AC} + 100$
$\Rightarrow \text{4AC} = 104$
$ \Rightarrow \boxed {\text{AC = 26 inches}}$
$\Rightarrow \text{AB = AC – 2}$
$\Rightarrow \text{AB} = 26 – 2$
$\Rightarrow \boxed{ \text{AB = 24 inches}}$
$\therefore$ The area of $\triangle \text{ABC} = \frac{1}{2} \times \text{Base} \times \text{Height}$
$\qquad \qquad = \frac{1}{2} \times \text{BC} \times \text{AB} = \frac{1}{2} \times 10 \times 24 = 120 \; \text{inches}^{2}$
Correct Answer $: 120$