Given that, in a car race, $\text{car A}$ beats $\text{car B}$ by $45 \; \text{km},$ and $\text{car B}$ beats $\text{car C}$ by $50 \; \text{km},$ and $\text{car A}$ beats $\text{car C}$ by $90 \; \text{km}.$
Let the distance over which the race has been conducted be $`x\text{’} \; \text{km}.$
$\textbf{Case 1:}$
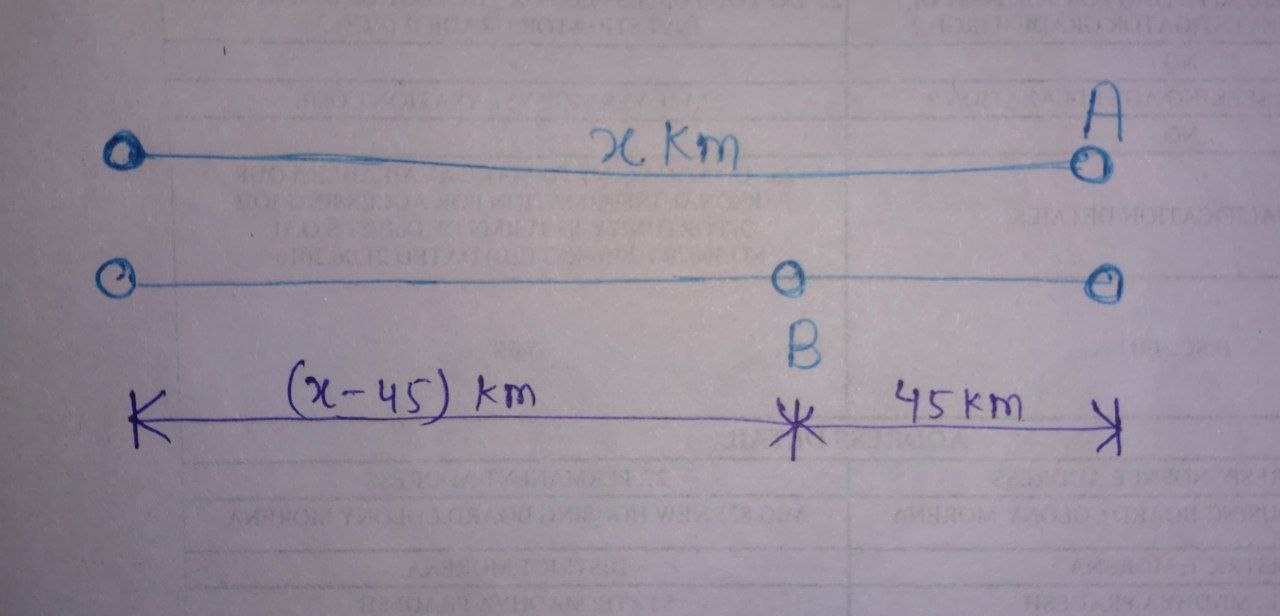
$\textbf{Case 2:}$
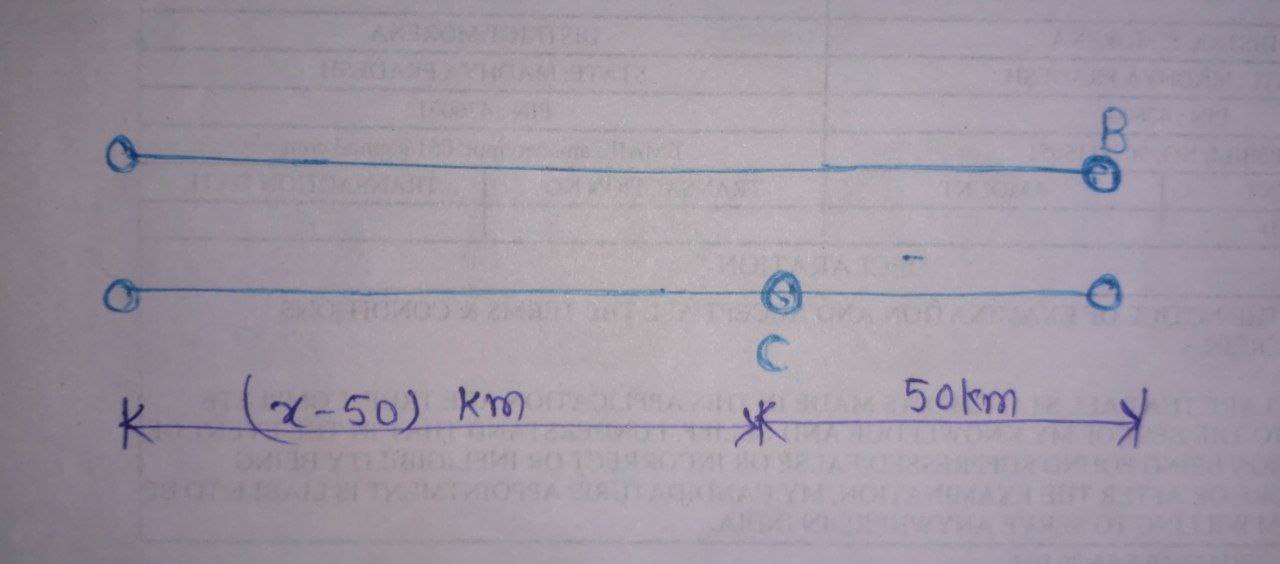
$\textbf{Case 3:}$
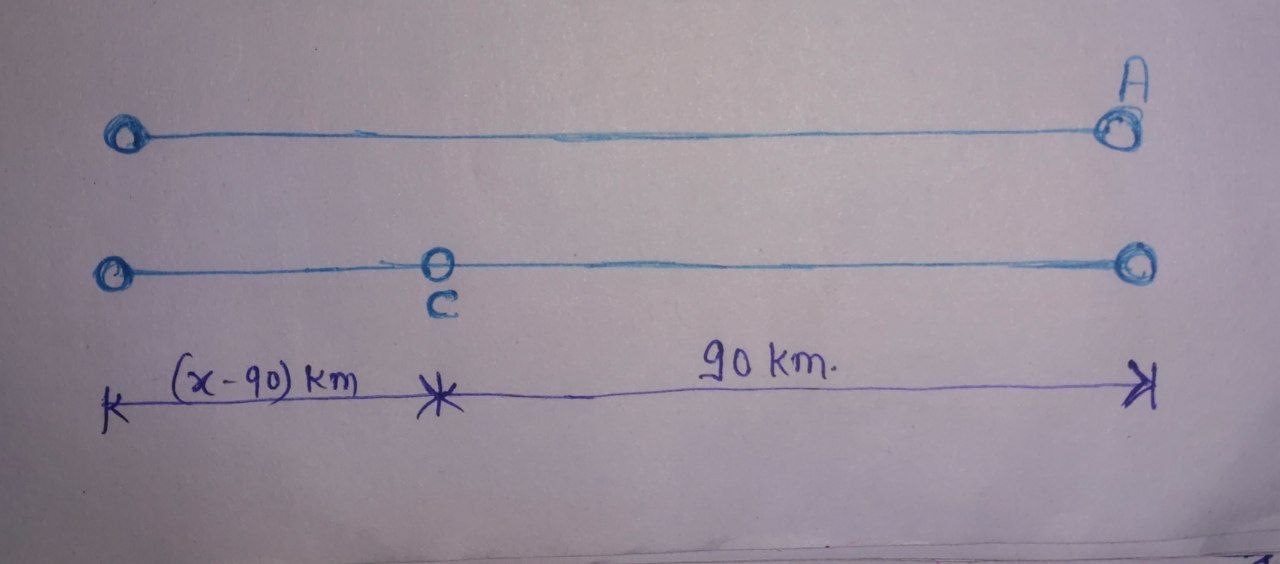
We know that, $ \text{Speed} = \frac{\text{Distance}}{\text{Time}} $
$\Rightarrow \boxed {\text{Speed} \propto \text{Distance}} \; (\text{Time = constant})$
Now, we can calculate the ratios of speed:
- In $\textbf{Case 1: } \frac{S_{A}}{S_{B}} = \frac{x}{x – 45} \quad \longrightarrow (1) $
- In $\textbf{Case 2: } \frac{S_{B}}{S_{C}} = \frac{x}{x – 50} \quad \longrightarrow (2) $
- In $\textbf{Case 3: } \frac{S_{A}}{S_{C}} = \frac{x}{x – 90} \quad \longrightarrow (3) $
Now, multiply equation $(1) \;\&\; (2),$ we get
$\left( \frac{S_{A}}{S_{B}} \right) \times \left( \frac{S_{B}}{S_{C}} \right) = \left( \frac{x}{x-45} \right) \left( \frac{x}{x-50} \right) $
$ \Rightarrow \frac{S_{A}}{S_{C}} = \frac{x^{2}}{(x-45)(x-50)} $
$ \Rightarrow \frac{x}{x-90} = \frac{x^{2}}{(x-45)(x-50)} \quad [\because \text{From equation (3)}]$
$ \Rightarrow (x-45)(x-50) = x(x-90) $
$ \Rightarrow x^{2} – 50x – 45x + 2250 = x^{2} – 90x $
$ \Rightarrow – 95x + 90x = – 2250 $
$ \Rightarrow -5x = -2250 $
$ \Rightarrow x = \frac{2250}{5} $
$ \Rightarrow \boxed{x = 450 \; \text{km}}$
$\therefore$ The distance (in km) over which the race has been conducted is $450.$
Correct Answer$: \text{D}$