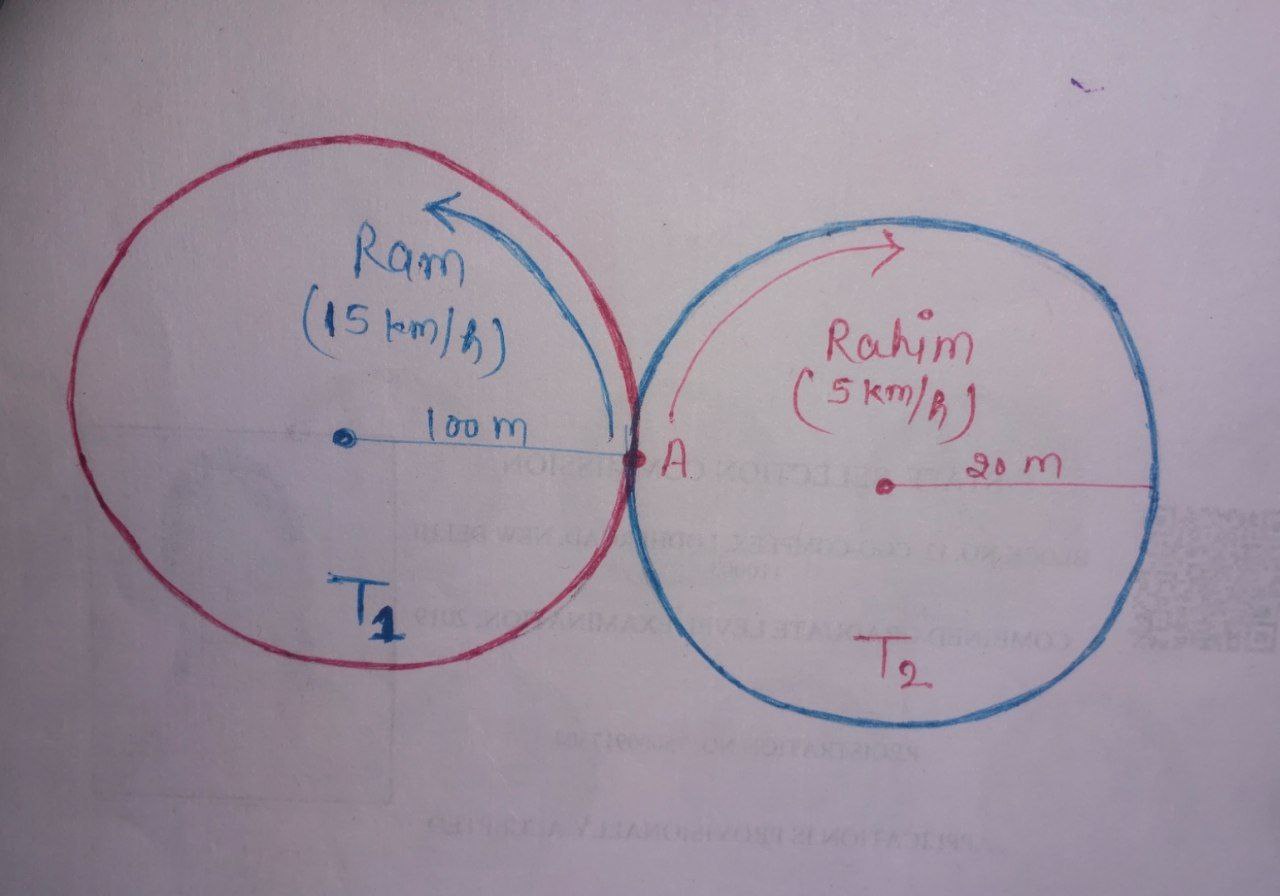
Given that, radii of circular tracks $\text{T}_{1} = 100 \; \text{m},$ and radii of circular tracks $\text{T}_{2} = 20 \; \text{m}.$
We know that, $\text{Speed} = \frac{\text{Distance}}{ \text{Time}} $
Time taken by each of then to complete one round $ = \frac{\text{Circumference of the circle}}{\text{Speed}}$
So, time taken by Ram to cover one round $ = \frac{2 \pi (100)}{15 \times \frac{5}{18}} = 48 \pi $
Time taken by Rahim to cover one round $ = \frac{2 \pi (20)}{5 \times \frac{5}{18}} = \frac{144 \pi}{5} $
Time taken by Ram and Rahim meet each other for the first time $ = \text{LCM} (48 \pi , \frac{144 \pi}{5})= 144 \pi $
$\therefore$ The number of full rounds that Ram makes before he meets Rahim for the first time $ = \frac{144 \pi}{48 \pi} = 3.$
$\textbf{Second Method:}$
$\textbf{Speeds:}$
- $\text{S}_{T_{1}} = 15 \; \text{km/hr} = 15 \times \frac{1000}{60 \times 60} = 15 \times \frac{5}{18} = \frac{25}{6} \; \text{m/sec.}$
- $\text{S}_{T_{2}} = 5 \; \text{km/hr} = 5 \times \frac{1000}{60 \times 60} = 5 \times \frac{5}{18} = \frac{25}{18} \; \text{m/sec.}$
$\textbf{Distances:}$
- $\text{D}_{T_{1}} = 2 \pi (100) = 200 \pi \; \text{m} $
- $\text{D}_{T_{2}} = 2 \pi (20) = 40 \pi \; \text{m} $
We know that, $\text{Speed} = \frac{\text{Distance}}{ \text{Time}} \Rightarrow \text{Time} = \frac{\text{Distance}}{ \text{Speed}} $
$\textbf{Time:}$
- $\text{T}_{T_{1}} = \frac{\text{D}_{T_{1}}} {\text{S}_{{T_{1}}}} = \frac{200 \pi}{ \frac{25}{6}} = 48 \pi $
- $\text{T}_{T_{2}} = \frac{\text{D}_{T_{2}}} {\text{S}_{{T_{2}}}} = \frac{40 \pi}{\frac{25}{18}} = \frac{144}{5} \pi $
Ratio of the time taken by Ram : Rahim $ = 48 \pi : \frac{144 \pi}{5} = 5 : 3 $
Time taken by Ram and Rahim to meet each other first time $ = \text{LCM} (5,3) = 15 \; \text{sec.}$
$\therefore$ Number of rounds made by Ram before he meets to Rahim for the first time $ = \frac{15}{5} = 3.$
Correct Answer$: \text{B}$