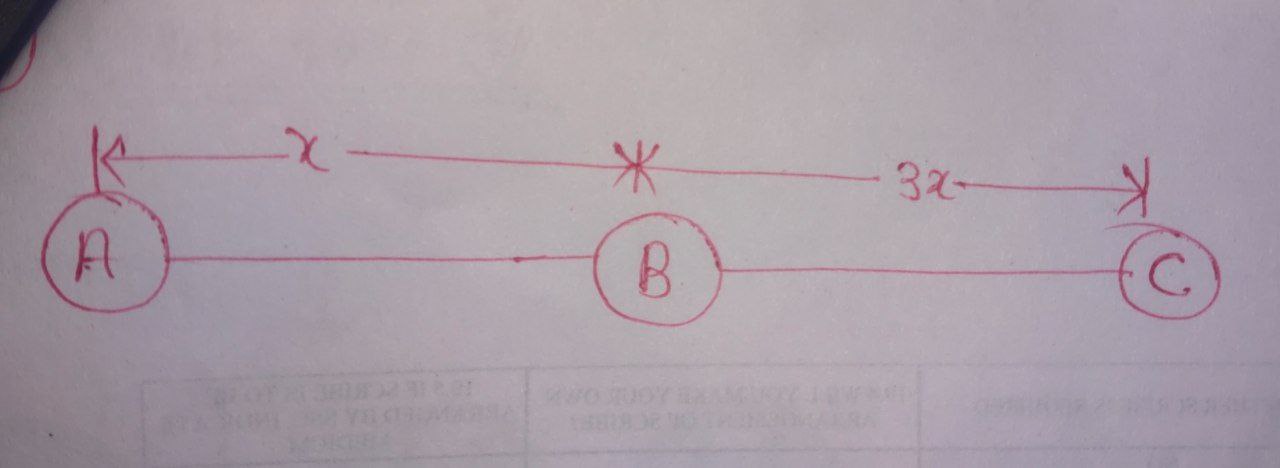
Let the distance between $\text{A}\; \&\; \text{B}$ be $`x\text{’} \; \text{km}.$ So, the distance between $\text{B} \;\&\; \text{C}$ be $`3x\text{’} \; \text{km}.$
we know that, $\text{Speed} = \frac{\text{Distance}}{\text{Time}} $
$ \Rightarrow \boxed{ \text{Time} = \frac{\text{Distance}}{ \text{Speed}}} $
Let total time taken by train $1$ and train $2$ be $\text{t}_{1} \; \text{hr}$ and $\text{t}_{2} \; \text{hr}$ respectively.
$\text{A} \longrightarrow \text{B} :$
- $\text{Speed of train 1} = \text{s} \; \text{km/hr}$
- $\text{Speed of train 2} = \text{2s} \; \text{km/hr}$
$\text{B} \longrightarrow \text{C} :$
- $\text{Speed of train 1} = \text{2s} \; \text{km/hr}$
- $\text{Speed of train 2} = \text{s} \; \text{km/hr}$
Total time taken by train $1 :$
$\text{t}_{1} = \left( \frac{x}{\text{s}} \right) + \left( \frac{3x}{\text{2s}} \right) $
$ \Rightarrow \text{t}_{1} = \frac{2x+3x}{\text{2s}} $
$ \Rightarrow \boxed{\text{t}_{1} = \frac{5x}{\text{2s}} \; \text{hr}} $
Total time taken by train $2 :$
$\text{t}_{2} = \left( \frac{x}{\text{2s}} \right) + \left( \frac{3x}{\text{s}} \right) $
$ \Rightarrow \text{t}_{2} = \frac{x+6x}{\text{2s}} $
$ \Rightarrow \boxed{\text{t}_{2} = \frac{7x}{\text{2s}} \; \text{hr}} $
Now, $ \dfrac{\text{t}_{1}}{\text{t}_{2}} = \dfrac{ \left(\frac{5x}{\text{2s}} \right)} {\left( \frac{7x}{\text{2s}} \right)} = \left( \frac{5x}{\text{2s}} \right) \times \left( \frac{\text{2s}}{7x} \right) = \frac{5}{7} $
$\therefore$ The required ratio of time $\text{t}_{1} : \text{t}_{2} = 5 : 7.$
Correct Answer$: \text{C}$