Given that, $ f(x) = x^{2} + ax + b \quad \longrightarrow (1) $
$ g(x) = f(x+1) – f(x-1) \quad \longrightarrow (2) $
From equation $(1),$ we can write,
- $ f(x+1) = (x+1)^{2} + a(x+1) +b $
- $ f(x-1) = (x-1)^{2} + a(x-1) + b $
Now, from equation $(2),$
$ g(x) = (x+1)^{2} + a(x+1) + b – [ (x-1)^{2} + a(x-1) + b] $
$ \Rightarrow g(x) = x^{2} + 2x + 1 + ax + a + b – [ x^{2} – 2x + 1 + ax – a + b] $
$ \Rightarrow g(x) = x^{2} + 2x + 1 + ax + a + b – x^{2} + 2x - 1 - ax + a - b $
$ \Rightarrow g(x) = 4x + 2a \quad \longrightarrow (3) $
we have, $ g(20) = 72 $
So, $ g(20) = 4 (20) + 2a $
$ \Rightarrow 80 + 2a = 72 $
$ \Rightarrow 2a = -8 $
$ \Rightarrow \boxed{a = – 4} $
We have $ f(x) \geq 0 $
$ x^{2} – 4x + b \geq 0 $
For this one graph will be
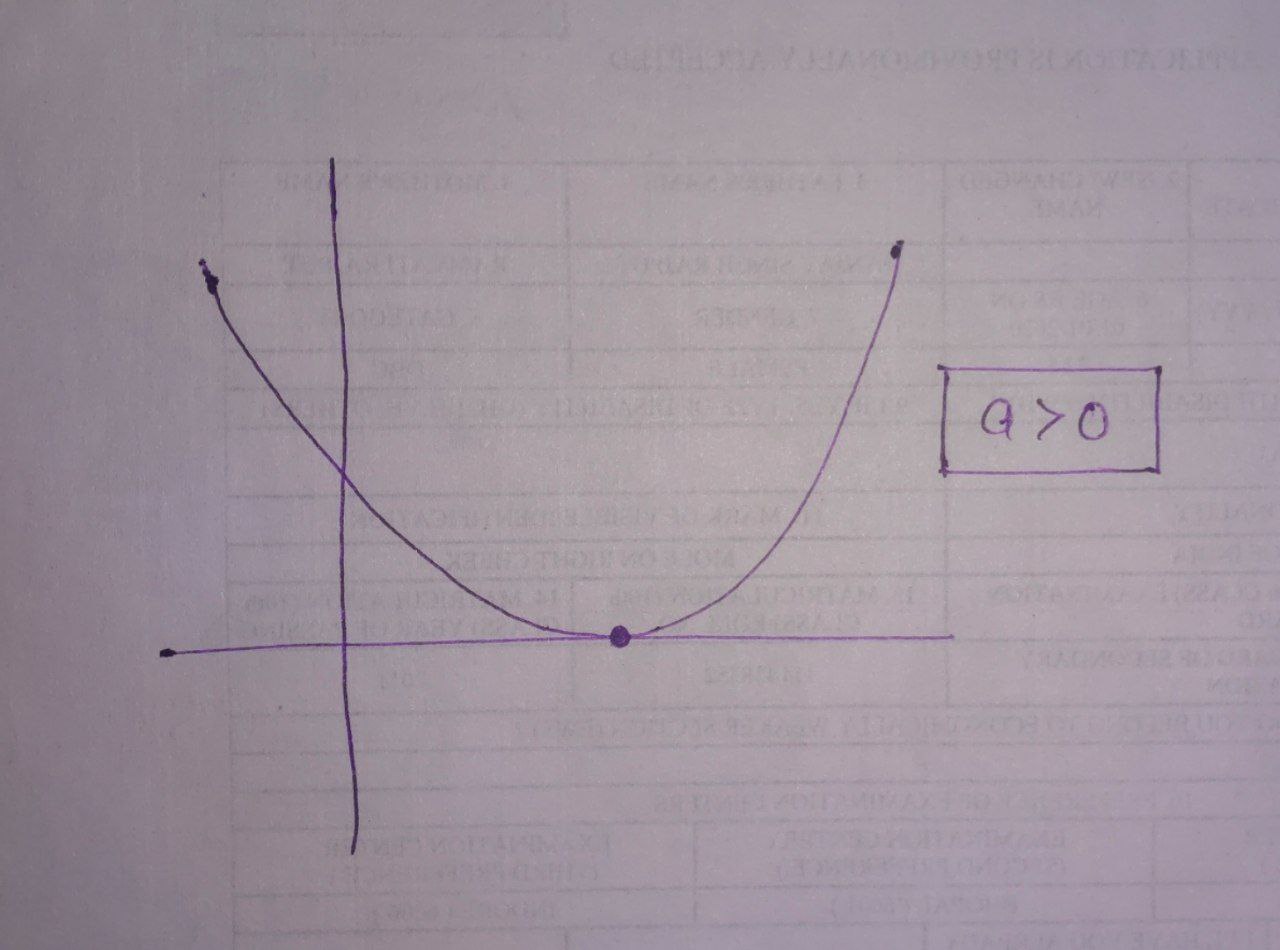
In this case graph can touch $x – \text{axis},$ so it can have at most one root.
Thus, discriminant $ \boxed{ \text{D} \leq 0} $
$ \Rightarrow \boxed{ b^{2} – 4ac \leq 0} $
$ \Rightarrow (-4)^{2} – 4 (1)(b) \leq 0 $
$ \Rightarrow 16 – 4b \leq 0 $
$ \Rightarrow 16 \leq 4b $
$ \Rightarrow 4b \geq 16 $
$ \Rightarrow \boxed{b \geq 4} $
So, least value of $b=4.$
$\therefore$ The smallest possible value of $b$ is $4.$
Correct Answer$: \text{D}$