Let the side of the equilateral triangle be $x.$
Let us consider an equilateral $\triangle \text{ABC, I}$ be interior point such that, $\text{ID, IE,}$ and $\text{IF}$ are perpendicular to sides $\text{BC, AC,}$ and $\text{AB}$ respectively.
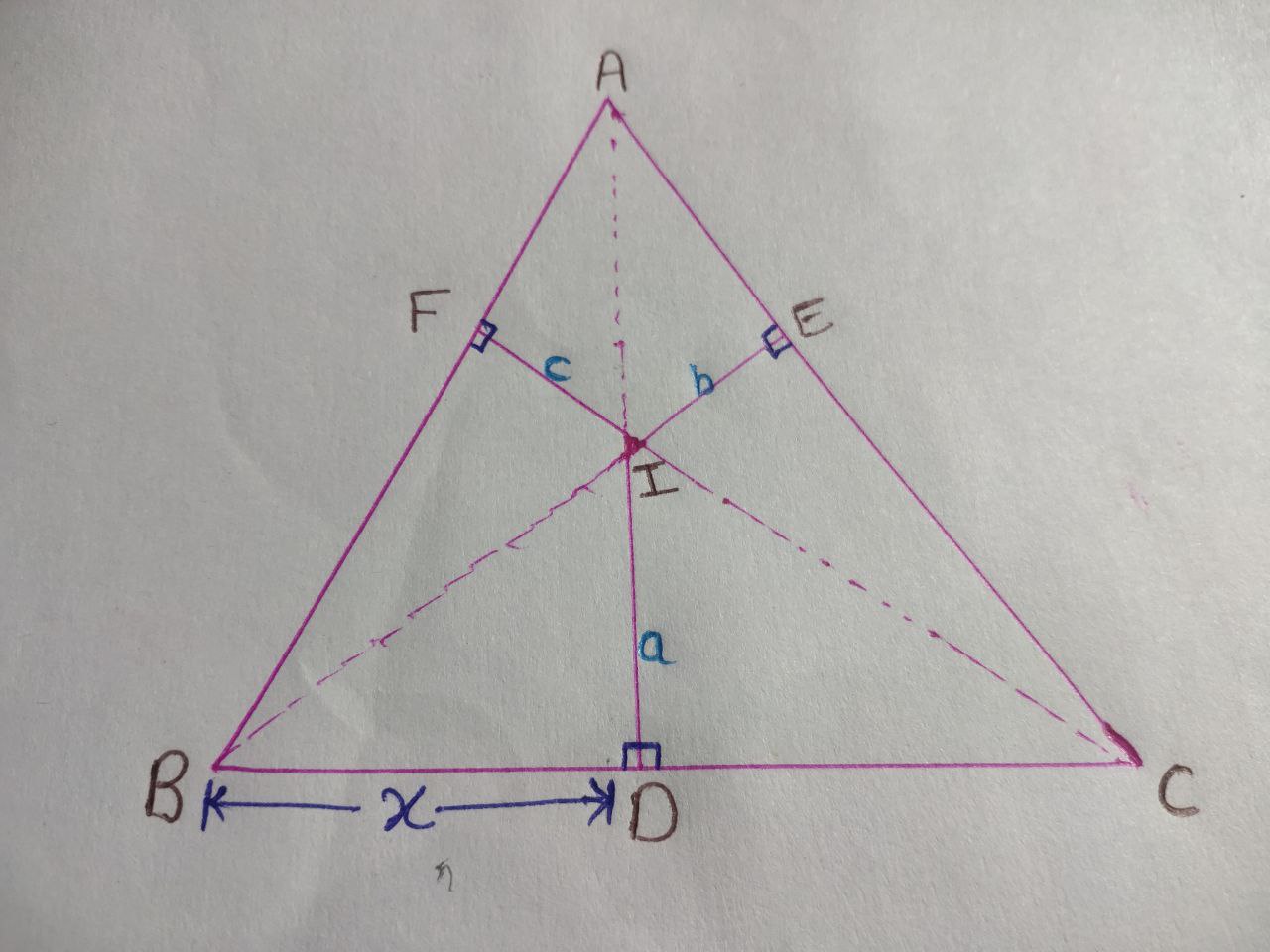
And, let $ \text{ID}= a, \text{IE}= b, \text{IF}= c.$
Also, $a+b+c = c$
Now, $ \text{Area of ABC} = \text{area of} \; \triangle \text{AIC} + \text{area of} \; \triangle \text{BIC} + \text{area of} \; \triangle \text{AIB}.$
$ \qquad \qquad = \frac{1}{2} \times x \times b + \frac{1}{2} \times x \times a + \frac{1}{2} \times x \times c $
$\qquad \qquad = \frac{1}{2} \times x (a+b+c) \; [\because a+b+c = s]$
$\qquad \qquad = \dfrac{xs}{2} \quad \longrightarrow (1)$
We know that, area of equilateral triangle $ = \dfrac{\sqrt{3}}{4} \times \text{(side)}^{2}$
Now, $ \dfrac{\sqrt{3}}{4} \times x^{2} = \dfrac{xs}{2} \quad [\because \text{From equation (1)}]$
$ \Rightarrow \boxed{ x = \frac{2s}{\sqrt{3}}}$
$\therefore$ The area of an equilateral triangle $ = \dfrac{\sqrt{3}}{4} \times x^{2}$
$\qquad \qquad = \dfrac{\sqrt{3}}{4} \times \left( \dfrac{2s}{\sqrt{3}} \right)^{2}$
$\qquad \qquad = \dfrac{\sqrt{3}}{4} \times \dfrac{2s}{\sqrt{3}} \times \dfrac{2s}{\sqrt{3}}$
$\qquad \qquad = \dfrac{s^{2}}{\sqrt{3}} \; \text{unit}^{2}.$
Correct Answer $: \text{B}$