Given that, area of rectangular metal sheet $ = 135 \; \text{sq inches}.$
Now, we can draw the diagram.
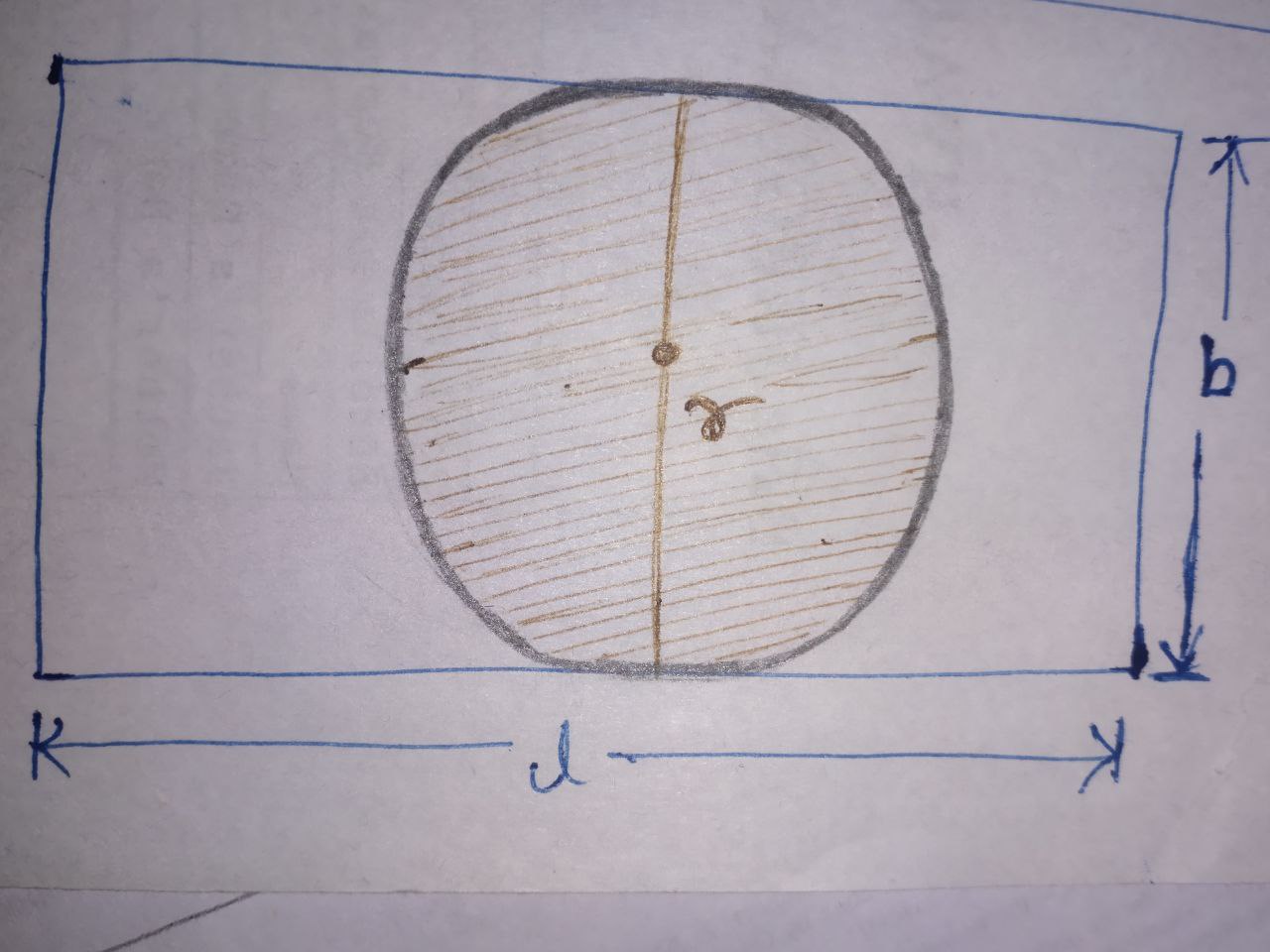
Let the length and breadth of the rectangle be $l$ and $b$ respectively.
Let the radius of a circle be $r \; \text{inches}.$
$\Rightarrow lb = 135$
Let the painted area be $3x.$ Then left unpainted area will be $2x.$
So, $3x + 2x = 135$
$\Rightarrow 5x = 135$
$ \Rightarrow \boxed{x = 27}$
The painted area (area of circle) $ = 3 \times 27 = 81 \; \text {sq inches}.$
The left unpainted area $ = 2 \times 27 = 54 \; \text{sq inches}.$
Now, $ \pi r^{2} = 81 $
$ \Rightarrow r = \frac{9}{\sqrt{\pi}}$
$ \Rightarrow b = 2r $
$ \Rightarrow \boxed {b = \frac{18}{\sqrt{\pi}}}$
And, $lb = 135$
$ \Rightarrow l \left( \frac{18}{\sqrt{\pi}} \right) = 135 $
$ \Rightarrow \boxed{l = \frac{15 \sqrt{\pi}}{2}}$
$\therefore$ The perimeter of the rectangle $ = 2 ( l+b)$
$ \qquad \qquad = 2 \left( \frac{15 \sqrt{\pi}}{2} + \frac{18}{ \sqrt{\pi}}\right) $
$\qquad \qquad = 15 \sqrt{\pi} + \frac{36}{\sqrt{\pi}}$
$\qquad \qquad = 15 \sqrt{\pi} + \frac{36}{\sqrt{\pi}} \times \frac{\sqrt{\pi}}{\sqrt{\pi}}$
$\qquad \qquad = 3 \sqrt{\pi} \left( 5 + \frac{12}{\pi} \right) \; \text{inches}.$
Correct Answer$: \text{C}$