First, we can draw the diagram. Let the volume of big circular cone and small circular cone be $V_{2}\; \text{cc}$ and $V_{1} \; \text{cc},$ respectively.
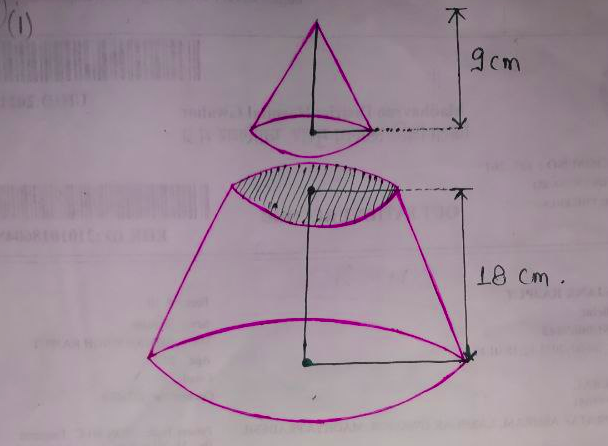
Let the volume of original cone be $V_{0} \; \text{cc}.$
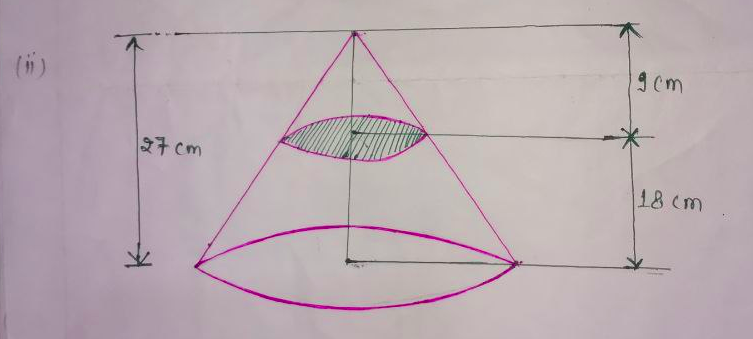
we can take the front view of the right circular cone.
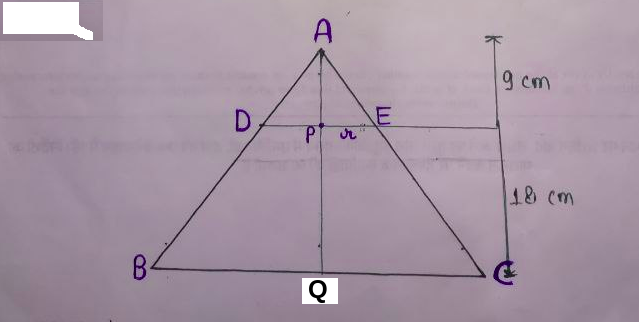
$\triangle \text{APE} \sim \triangle \text{AQC}$
So, $\frac{\text{AP}}{\text{AQ}} = \frac{\text{PE}}{\text{QC}} = \frac{9}{27} = \frac{1}{3}$
Let $\text{PE} = r \; \text{cm},$ then $\text{QC} = 3r \; \text{cm}$
Given that, $V_{2} – V_{1} = 225 \quad \longrightarrow (1)$
Now, $V_{0} = \frac{1}{3} \pi (3r)^{2} \cdot 27$
$ \Rightarrow V_{0} = \frac{1}{3} \pi 9r^{2} \cdot 27$
$ \Rightarrow \boxed{V_{0} = 81 \pi r^{2}} \quad \longrightarrow (2)$
And, $V_{1} = \frac{1}{3} \pi (r)^{2} \cdot 9$
$ \Rightarrow \boxed{V_{1} = 3 \pi r^{2}}$
And, $V_{2} = V_{0} – V_{1} = 81 \pi r^{2} – 3 \pi r^{2}$
$ \Rightarrow \boxed{ V_{2} = 78 \pi r^{2}}$
Put the value of $V_{1}$ and $V_{2}$ in the equation $(1),$ we get
$V_{2} – V_{1} = 225$
$ \Rightarrow 78 \pi r^{2} – 3 \pi r^{2} = 225$
$ \Rightarrow 75 \pi r^{2} = 225$
$ \Rightarrow \boxed{\pi r^{2} = 3}$
Now, from the equation $(2).$
$V_{0} = 81 \pi r^{2}$
$ \Rightarrow V_{0} = 81 \times 3$
$ \Rightarrow \boxed{ V_{0} = 243 \; \text{cc}}$
$\textbf{Short Method:}$
Given that, $h_{l} = 27 \; \text{cm}, h_{s} = 9 \; \text{cm}$
So, $\dfrac{h_{s}}{h_{l}} = \dfrac{9}{27} = \dfrac{1}{3}$
$\Rightarrow \dfrac{r_{s}}{r_{l}} = \dfrac{h_{s}}{h_{l}} = \dfrac{1}{3}$
Then, $\dfrac{V_{s}}{V_{l}} = \left( \dfrac{1}{3} \right)^{3} = \dfrac{1}{27}$
Let the volume of the larger cone (original cone) be $27x.$
Then the volume of the smaller cone will be $x.$
So,
- $V_{0} = 27x$
- $V_{1} = x$
Then, $V_{2} = V_{0} – V_{1}$
$\Rightarrow V_{2} = 27x – x$
$ \Rightarrow \boxed{ V_{2} = 26x}$
We have, $V_{2} – V_{1} = 225$
$ \Rightarrow 26x – x = 225$
$ \Rightarrow 25x = 225$
$ \Rightarrow \boxed{x = 9}$
$\therefore V_{0} = 27x = 27 \times 9 = 243 \; \text{cc}.$
Correct Answer $: \text{D}$