CAT 2006 | Question: 71

Question

A semi-circle is drawn with $\text{AB}$ as its diameter. From $\text{C}$, a point on $\text{AB,}$ a line perpendicular to $\text{AB}$ is drawn meeting the circumference of the semi-circle at $\text{D.}$ Given that $\text{AC = 2 cm}$ and $\text{CD = 6 cm}$ the area of the semi-circle (in sq. cm) will be

• A. $32 \pi$
• B. $50 \pi$
• C. $40.5 \pi$
• D. $81 \pi$
• E. undeterminable

Answer 1

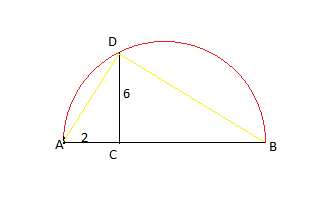
Let CB = x cm.

From triangle  ACD, where angle ACD = 90'.

AD^2 = AC^2 + CD^2

          = 2 ^2 + 6 ^2

          =40.    -----------------(P) 

From triangle BCD, where angle BCD = 90'.

BD^2 = CB ^2 + CD ^2

           = x ^2 + 6 ^2 ---------(Q)

From triangle ABD, where angle ADB = 90'.

AB^2 = AD ^2 + BD ^2

=> (2 + x)^2 = 40+ (x^2+ 36)                  //from eqn- P and Q.

=> 4 + 4x + x ^2= 76 + x^2

=>  x = 72/4 = 18.

Diameter of cemi-circle = 2 + x = 2 + 18 = 20.

So, radius = 10 cm. 

Hence, area of semi-circle = $\pi$(10 ^2 ) / 2.

                                                 = $50\pi$.

Ans- 2.