Correct Answer: (D)
Explanation:
This game introduces the idea of reciprocal causation. For example, the constraint that says “If A, then B, and if B, then A” should be transcribed in one of the following two ways, based on the configurations of the other variables in the diagram:

You will run into reciprocal causation in the final constraint of this logic game. Here are the final diagrams that you should create:
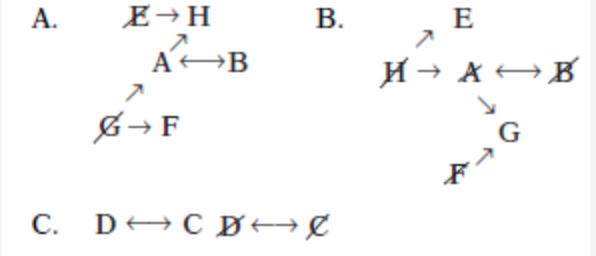
Notice how the reciprocal causation constraints are diagrammed. Be aware of the implications of these constraints. For instance, if $B$ is not sent (diagram B), then $A$ cannot be sent and $G$ must be sent. In diagram A, if $B$ is sent, then $A$ and $H$ are sent.
What is the greatest number of pilots that could be sent to negotiate?
(D) It is possible, using diagrams A and C, to see that all eight plots could be sent to negotiate.