Correct Answer: A
Explanation:
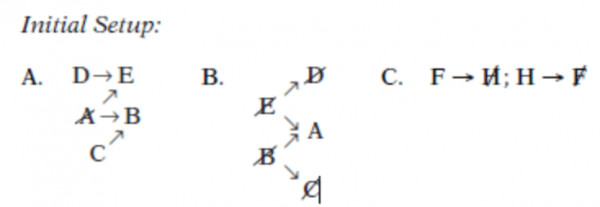
Who could be the only person in the hideout?
(A) $A$ could be the only person in the hideout, as shown in diagram B. While $F$ and $H$ cannot be in the hideout at the same time, they can be out at the same time.
(B) If $E$ is out, then $A$ is in.
(C) If $B$ is out, then $A$ is in.
(D, E) If $E$ or $B$ is out, then $A$ must be in. This means that $A$ must accompany $H$ or $G$ so long as either $E$ or $B$ is out. Therefore, we know (A) must be the correct answer.