Correct Answer: (C)
Explanation:
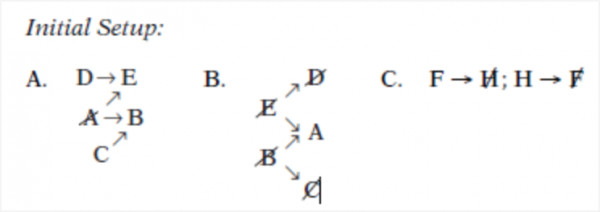
If $F$ must be in the hideout when $A$ or $B$ is in the hideout, then which of the following must be true?
(C) This question adds a constraint to the game, and you should add marks to your diagrams to represent this additional constraint. It is generally not wise to add marks directly to your diagram from individual questions, since these question-constraints will not influence the game aside from that one question. Many people still mark the question-constraint in pencil and then erase it after the question is over. Here is what your diagram would look like:
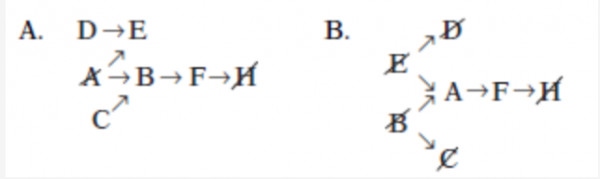
You see in both scenarios that $F$ must be in the hideout and $H$ must be out of the hideout.
(A) Negation possible in diagram B.
(B) Negation possible in diagram B.
(D) Negation possible in diagram B.
(E) C is the correct answer.