Let $r$ be the radius of the third circle. Then,
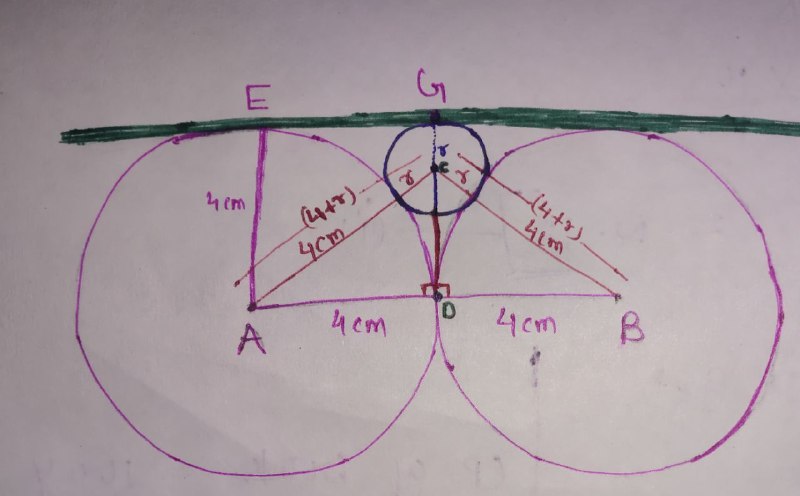
From the above diagram, we get
$AE= GC + CD$
$\Rightarrow 4 = r + CD $
$ \Rightarrow CD = ( 4-r )$
In $ \triangle ADC,$
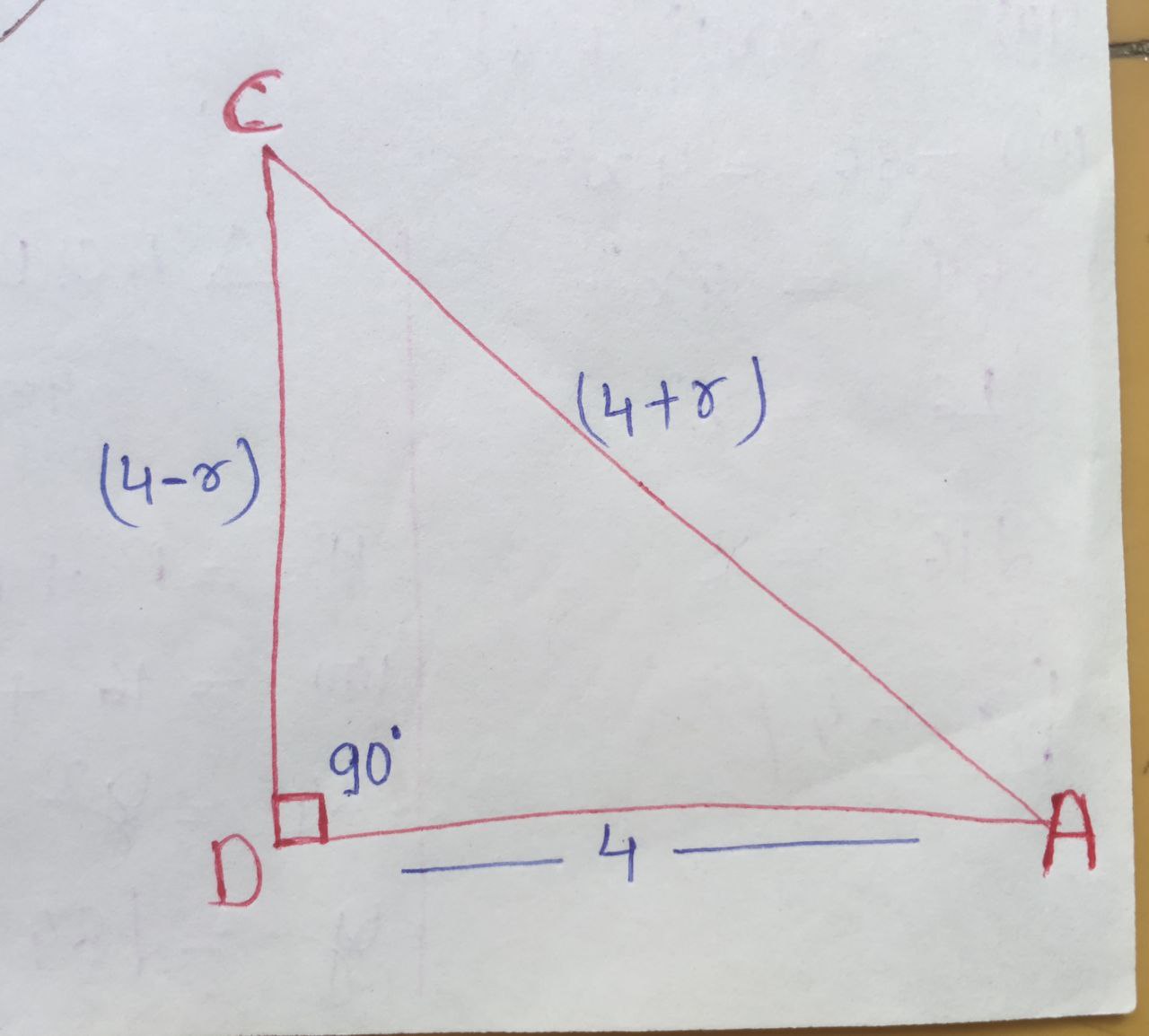
$ \angle D = 90^{\circ},$ using Pythagoras theorem.
$ \boxed{(AC)^{2} = (CD)^{2} + (AD)^{2}} $
$(4+r)^{2} = (4-r)^{2} + (4)^{2}$
$ \Rightarrow 16 + r^{2} + 8r = 16 + r^{2} – 8r + 16$
$ \Rightarrow 8r = -8r + 16 $
$\Rightarrow 8r + 8r = 16$
$ \Rightarrow 16r = 16$
$ \Rightarrow r = 1$
$ \therefore $ The radius of the third circle is $1\;\text{cm}.$
Correct Answer: D