Given that, $\triangle ABC$ is a right-angled triangle.
Let $\angle A = 90^{\circ}$
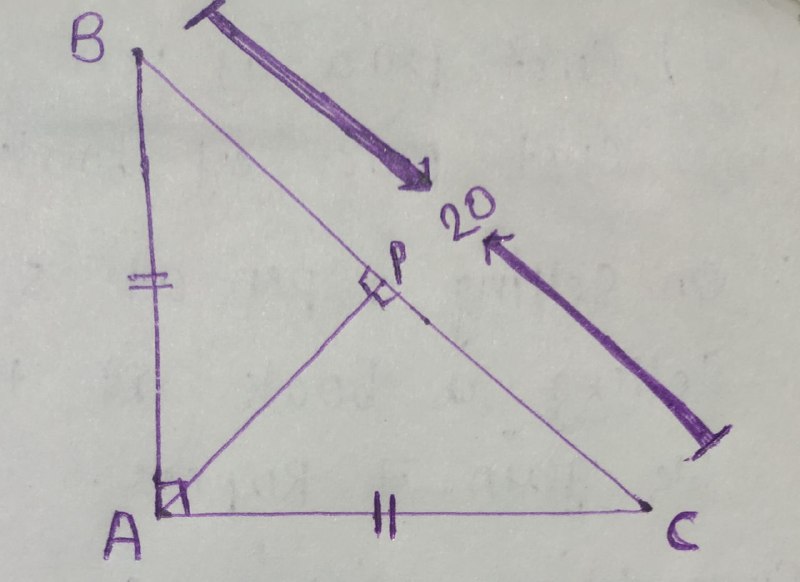
For $AP$ to be maximum triangle $ABC$ has to be an isosceles triangle. Means $AB = AC$
Apply the Pythagorean theorem, in $\triangle ABC.$
$\boxed {\text{Hypotenuse(H)}^{2} = \text{Perpendicular (P)}^{2} + \text{Base (B)}^{2}}$
$(20)^{2} = (AB) ^{2} + (AC)^{2}$
$ \Rightarrow 400 = 2 AB^{2} \quad [\because AB = AC]$
$ \Rightarrow 200 = AB^{2}$
$ \Rightarrow \sqrt{200}= AB$
$ \Rightarrow AB =10 \sqrt {2} $
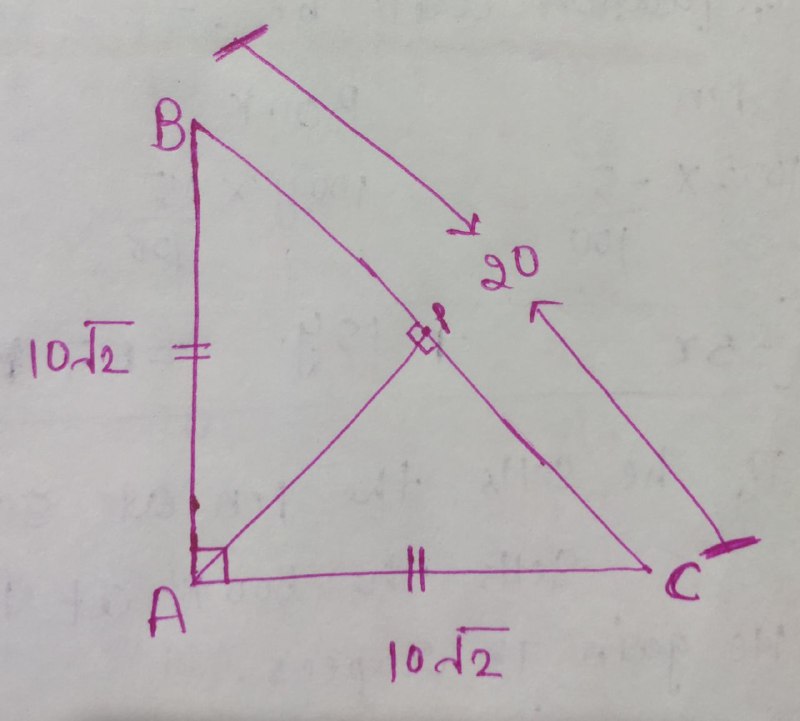
We have, $ \triangle{ APB } = \triangle {APC} $
Then, the area also should be equal.
$ \dfrac{1}{2} AC \times BA = \dfrac {1}{2} BC \times AP$
$ \Rightarrow \boxed {\dfrac{AC\times BA}{BC} = AP}$
$ \Rightarrow \dfrac {10 \sqrt{2} \times 10 \sqrt {2}}{20}=AP$
$ \Rightarrow \dfrac{100 \times 2}{20}=AP$
$\Rightarrow AP=10\;\text{cm}.$
Correct Answer: A