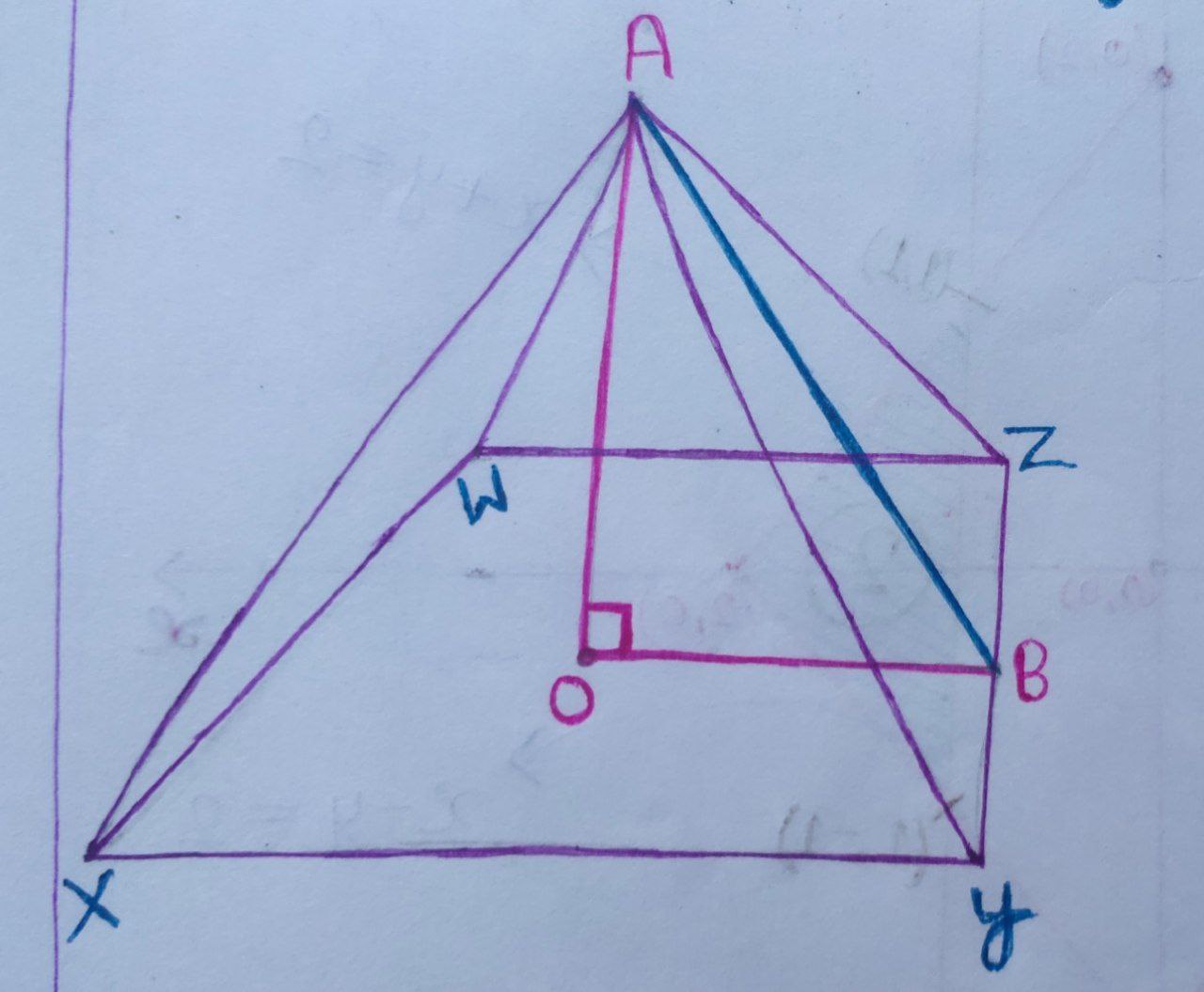
We can draw the diagram, using the given information in the question.
The base of a regular pyramid is square. That means $\square\text{WXYZ}$ will be the square.
The four sides of a regular pyramid is an equilateral triangle. That means $\triangle \text{AXW}, \triangle \text{AWZ}, \triangle \text{AXY}$ and $\triangle \text{AYZ}$ are equilateral triangle, and side of each equilateral triangle is $20\; \text{cm}.$
Now, consider the $\triangle \text{AYZ}.$
Let $`h\text{’ cm}$ be the height of a triangle.
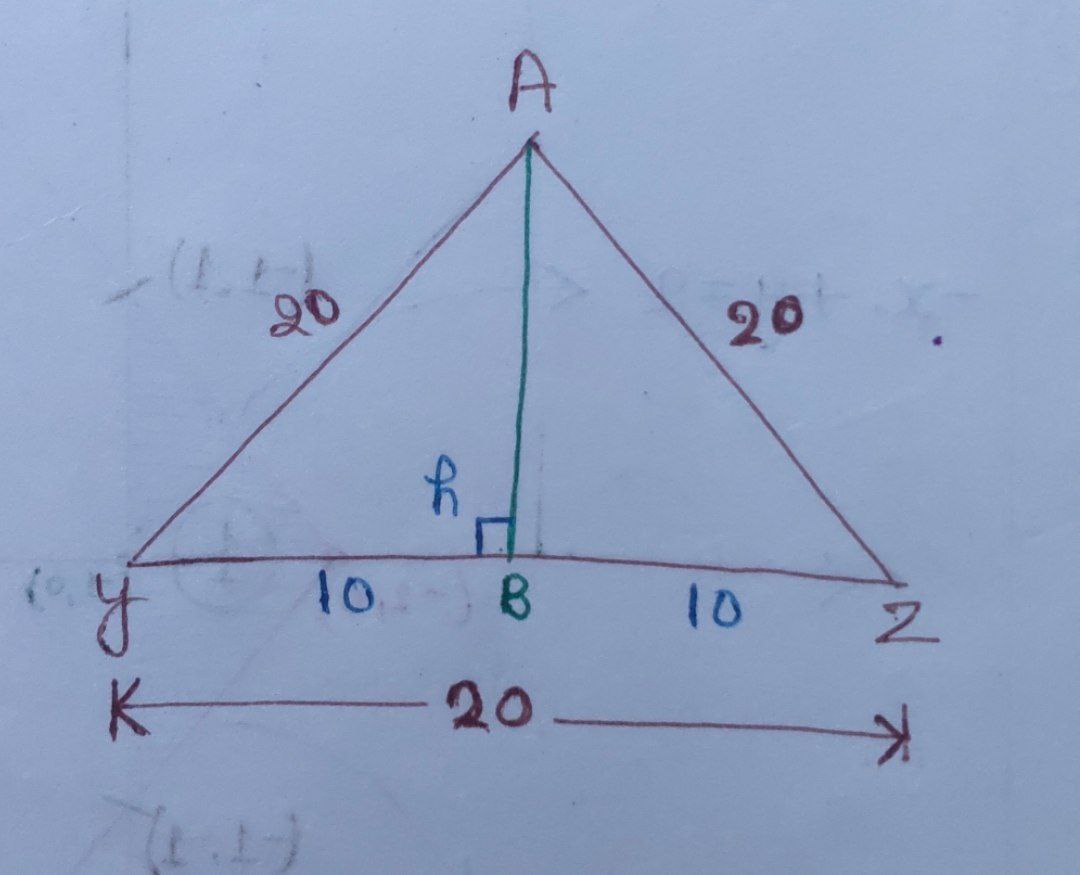
In $\triangle \text{ABY},$ using the Pythagoras’ theorem,
$\boxed{ \text{(AY)}^{2} = \text{(AB)}^{2} + \text{(YB)}^{2}}$
$ \Rightarrow (20)^{2} = (h)^{2} + (10)^{2}$
$ \Rightarrow 400 = h^{2} + 100$
$ \Rightarrow h^{2} = 300$
$ \Rightarrow h = \sqrt{300}$
$ \Rightarrow h = \sqrt{ 3 \times 100}$
$ \Rightarrow h = \text{AB} = 10 \sqrt{3}\; \text{cm}$
Here, $ \text{OB} = \frac{\text{side of the square}}{2} = \frac{\text{XY}}{2} = \frac{20}{2} = 10\; \text{cm}.$
In $ \triangle \text{AOB},$ using the Pythagoras’ theorem,
$ \text{(AB)}^{2} = \text{(OA)}^{2} + \text{(OB)}^{2}$
$ \Rightarrow (10 \sqrt{3})^{2} = \text{(OA)}^{2} + (10)^{2}$
$ \Rightarrow 300-100 = \text{(OA)}^{2}$
$ \Rightarrow \text{(OA)}^{2} = 200$
$ \Rightarrow \text{OA} = \sqrt{200} = \sqrt{2 \times 100} $
$ \Rightarrow \boxed {\text{OA} = 10 \sqrt{2}\; \text{cm}}$
$\therefore$ The vertical height of the pyramid $ = 10 \sqrt{2}\; \text{cm}.$
Correct Answer $: \text{D}$