Given that, $n^{3} – 11n^{2} + 32n – 28 > 0 \quad \longrightarrow (1) $
For, the factorazation, let us assume
$ n^{3} – 11n^{2} + 32n – 28 = 0 \quad \longrightarrow (2) $
Now, put the various of $n,$ and check
- $ n = – 1 \Rightarrow (-1)^{3} – 11(-1)^{2} + 32(-1) – 28 = 0 $
$ \qquad \qquad \quad \; \Rightarrow -1 -11 -32 -28 = 0 $
$ \qquad \qquad \quad \; \Rightarrow \boxed{ -72 \neq 0} $
- $n=0 \Rightarrow (0)^{3} – 11 (0)^{2} + 32(0) – 28 = 0 $
$ \qquad \qquad \quad \; \Rightarrow \boxed{ -28 \neq 0} $
- $n=1 \Rightarrow (1)^{3} – 11 (1)^{2} + 32(1) – 28 = 0 $
$ \qquad \qquad \quad \; \Rightarrow 1 – 11 + 32 – 28 = 0 $
$ \qquad \qquad \quad \; \Rightarrow \boxed{ – 6 = 0} $
- $n=2 \Rightarrow (2)^{3} – 11 (2)^{2} + 32(2) – 28 = 0 $
$ \qquad \qquad \quad \; \Rightarrow 8 – 44 + 64 – 28 = 0 $
$ \qquad \qquad \quad \; \Rightarrow 72 – 72 = 0 $
$ \qquad \qquad \quad \; \Rightarrow \boxed{0 = 0} $
So, $(n-2)$ is the factor.
Now, we can divide the whole expression by $ n-2.$
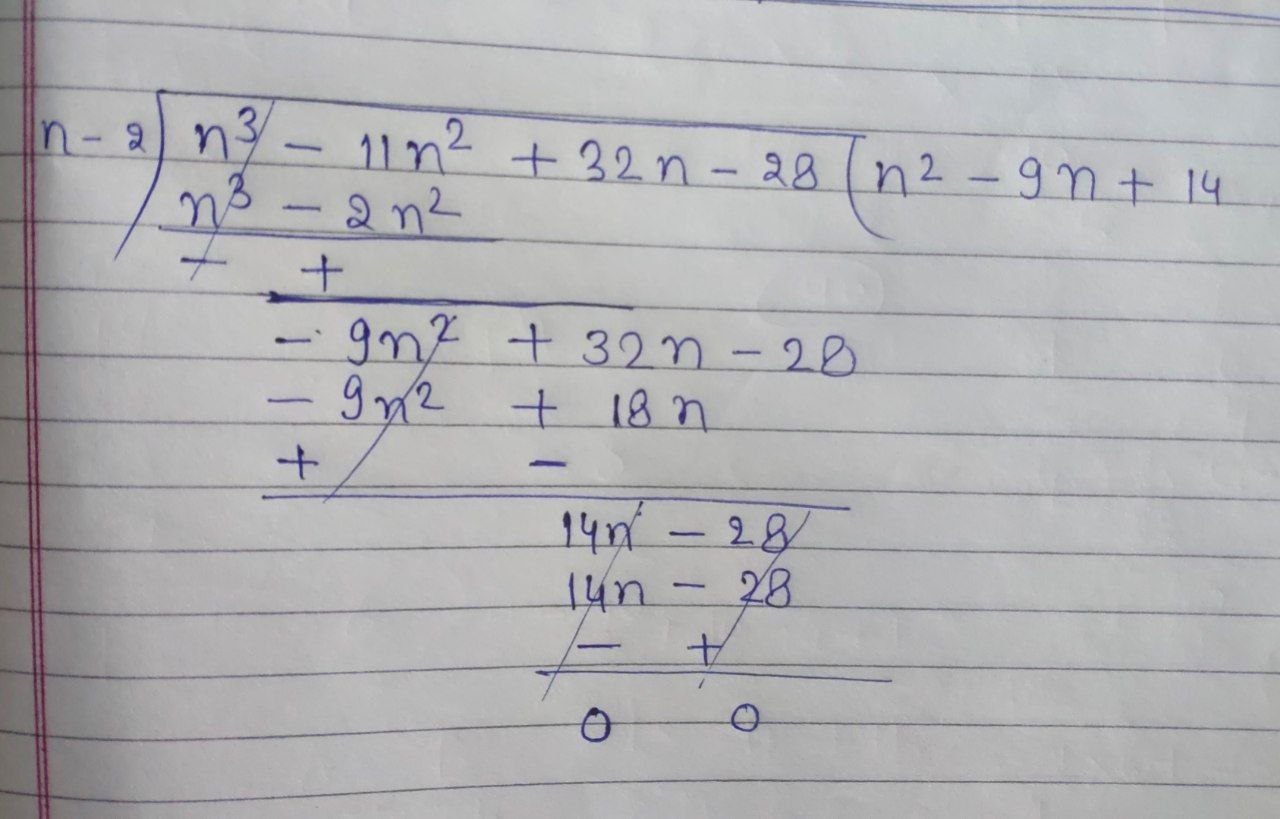
We can write, $ (n-2) (n^{2} -9n + 14) = 0 $
$ \Rightarrow (n-2) ( n^{2} – 7n – 2n + 14) = 0 $
$ \Rightarrow (n -2) \left[n (n-7) -2 (n – 7) \right] $
$ \Rightarrow (n – 2)(n – 2)(n – 7) = 0 $
$ \Rightarrow \boxed{n = 2, 2, 7} $
The $n = 7$, makes the whole expression zero.
So, $n = 8$ is the smallest integer which make expression greater than zero.
Put the value of $n = 8,$ in the equation $(1),$ we get
$ n^{3} – 11n^{2} + 32n – 28 > 0 $
$ \Rightarrow (8)^{3} – 11 (8)^{2} + 32 (8) – 28 > 0 $
$ \Rightarrow 512 – 704 + 256 – 28 > 0 $
$ \Rightarrow 768 – 732 > 0 $
$ \Rightarrow \boxed{36 > 0} $ (Satisfied)
$\therefore$ The value of smallest integer is $8.$
Correct Answer $:8$