Given that, $A$ and $B$ are two points such that $B$ is $350 \; \text{km}$ of $A.$
Let $`x\text{’}$ and $`y\text{’}$ be the speed $(\text{in km/hr})$ of cars starting from both $A$ and $B$ respectively.
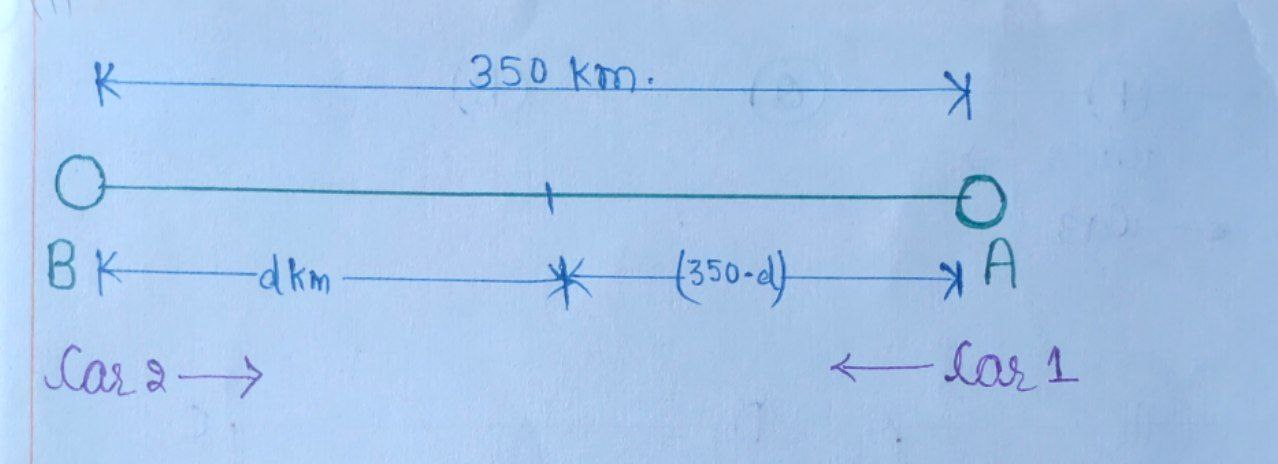
Let us assume $\text{car 2}$ traveled $ d\;\text{km}$ and meet $\text{car 1},$ after $1 \; \text{hour}.$
$\boxed{\text{Speed} = \frac{\text{Distance}}{\text{Time}}}$
So, $ S_{\text{car 1}} = \frac{350-d}{1} $
$\Rightarrow \boxed{x = 350 – d} \quad \longrightarrow (1) $
And, $ S_{\text{car 2}} = \frac{d}{1} $
$ \Rightarrow \boxed {y = d} $
From the equation $(1),$ we get
$ x = 350 – d $
$ \Rightarrow x = 350 – y $
$\Rightarrow \boxed{x+y = 350} \quad \longrightarrow (2) $

Let us assume, when they move toward east, they meet at point $P$ and distance traveled by $\text{car 1}$ is $`p\text{’} \; \text{km},$ and distance traveled by $\text{car 2}$ is $`350+p\text{’} \; \text{km}$ in $7 \; \text{hours}.$
So, $S_{\text{car 1}} = \text{p}{7} $
$ \Rightarrow x = \frac{p}{7} $
$ \Rightarrow \boxed{p = 7x} \quad \longrightarrow (3) $
And, $S_{\text{car 2}} = \frac{350+p}{7} $
$ \Rightarrow y = \frac{350+7x}{7} \quad [\because \text{From equation} (3)] $
$ \Rightarrow 7y = 350 + 7x $
$ \Rightarrow 7y – 7x = 350 $
$ \Rightarrow 7(y – x) = 350 $
$ \Rightarrow y – x = \frac{350}{7} $
$ \Rightarrow \boxed{y – x = 50 \; \text{km/hr}} $
$\textbf{PS:}$ If they both move in east direction, then $B$ will overtake $A$ only if $y>x.$
$\textbf{Short Method: }$
Concept of relative speed ;
- When two bodies moves in the same direction then the $ \boxed{\text{Relative speed = Difference of speeds}} $
- When two bodies move in opposite direction, then the $ \boxed { \text {Relative speed = Sum of speeds}} $
Let $`x\text{’}$ and $`y\text{’}$ be the speed ( in km/hr) of cars starting from both $A$ and $B$ respectively.

$\text{Relative speed} = (y – x) \; \text{km/hr} \quad [\because y > x] $
They travel $350 \; \text{km}$ in $7 \; \text{hours}$ with a relative speed of $(y – x) \; \text{km/hr}.$
So, $(y -x) = \frac{350}{7} $
$ \Rightarrow \boxed{ y – x = 50 \; \text{km/hr}} $
Correct Answer $: 50$