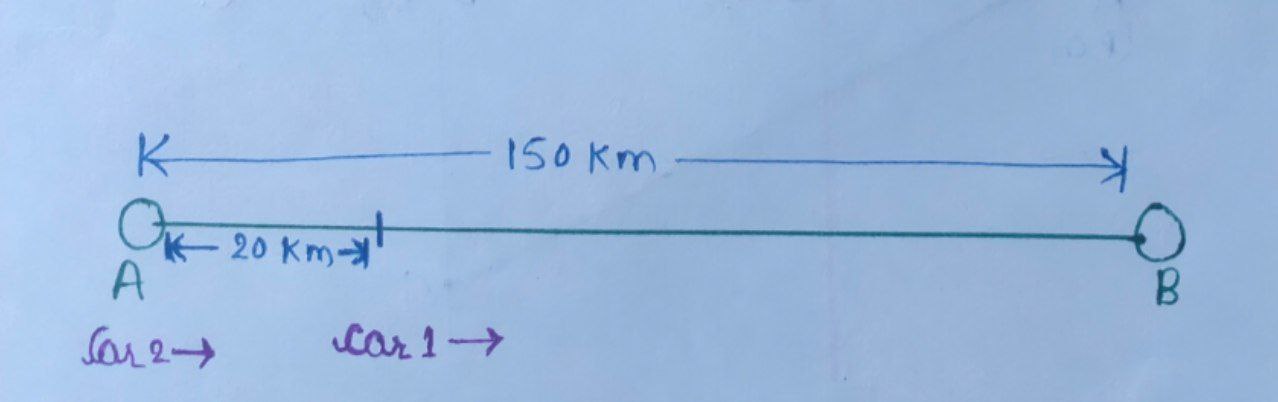
Given that, points $A$ and $B$ are $150 \; \text{km}$ apart.
Each car travel at a speed of $100 \; \text{km/hr}$ for the first $50 \; \text{km}.$
$ \boxed{\text{Time} = \frac{\text{Distance}}{\text{Speed}}} $
So, $ t_{1} = \frac{50}{100} $
$ \Rightarrow \boxed{t_{1} = \frac{1}{2} \; \text{hour}} $
And, each car travel at a speed of $ 50 \; \text{kmph}$ for the $50 \; \text{km}.$
So, $ t_{2} = \frac{50}{50} $
$ \Rightarrow \boxed{t_{2} = 1 \; \text{hour}} $
And, each travel at a speed of $25 \; \text{kmph}$ for the last $50 \; \text{km}. $
So, $t_{3} = \frac{50}{25} $
$ \Rightarrow \boxed{t_{2} = 2 \; \text{hours}} $
Thus, total time for $\text{car 1}$ and $\text{car 2}$ to reach from $A$ to $ B = t_{1} + t_{2} + t_{3} = \frac{1}{2} + 1 + 2 = 3.5 \; \text{hours} $
$\text{Car 1}$ is $20 \; \text{km}$ away from $A\;\text{(car 2)}.$
So, time taken by $\text{car 1}$ to cover first $20 \; \text{km} = \frac{20}{10} = \frac{1}{5} \; \text{hours} = 0 \cdot 2 \; \text{hours} = \frac{1}{5} \times 60 = 12 \; \text{minutes} $
So, $\text{car 2}$ is lagging by $12 \; \text{minutes}$ when $\text{car 1}$ reach point $B.$
If $\text{car 1}$ reaches $B,$ $\text{car 2}$ will take $12 \; \text{minutes}$ to reach $B.$
The distance between $\text{car 2}$ and $B = 25 \times \frac{1}{5} = 5 \; \text{km}.$
$\therefore$ The distance between $\text{car 2}$ and $B,$ when $\text{car 1}$ reaches $B$ is $5 \; \text{km}.$
$\textbf{Short Method} :$
Each part of the distance covers by both the cars, the speed is the same.
So, if both the cars start from the same point, and the start time is also the same, then they reach the destination at the same time.
But, here $\text{car 1}$ is $20 \; \text{km}$ ahead of $\text{car 2}.$
So, time taken by $\text{car 1}$ to travel first $ 20 \; \text{k} = \frac{20}{100} = \frac{1}{5} \; \text{hour} = \frac{1}{5} \times 60 = 12 \; \text{minutes} $
Thus, $\text{car 2}$ will reach $B, 12 \; \text{minutes}$ after $\text{car 1 }$ reach.
$\therefore$ The distance between $\text{car 2}$ and $ B = 25 \times \frac{1}{5} = 5 \; \text{km}. $
Correct Answer $: 5$