Given that,
- $ \text{T} = \{ 1,2,3,4\} $
- $ \text{Q} = \{ 2,3,5,6 \} $
- $ \text{R} = \{ 1,3,7,8,9\} $
- $ \text{S} = \{ 2,4,9,10\} $
$ \boxed{ \text{A} \triangle \text{B} = ( \text{A} \cup \text{B}) – ( \text{A} \cap \text{B})} $
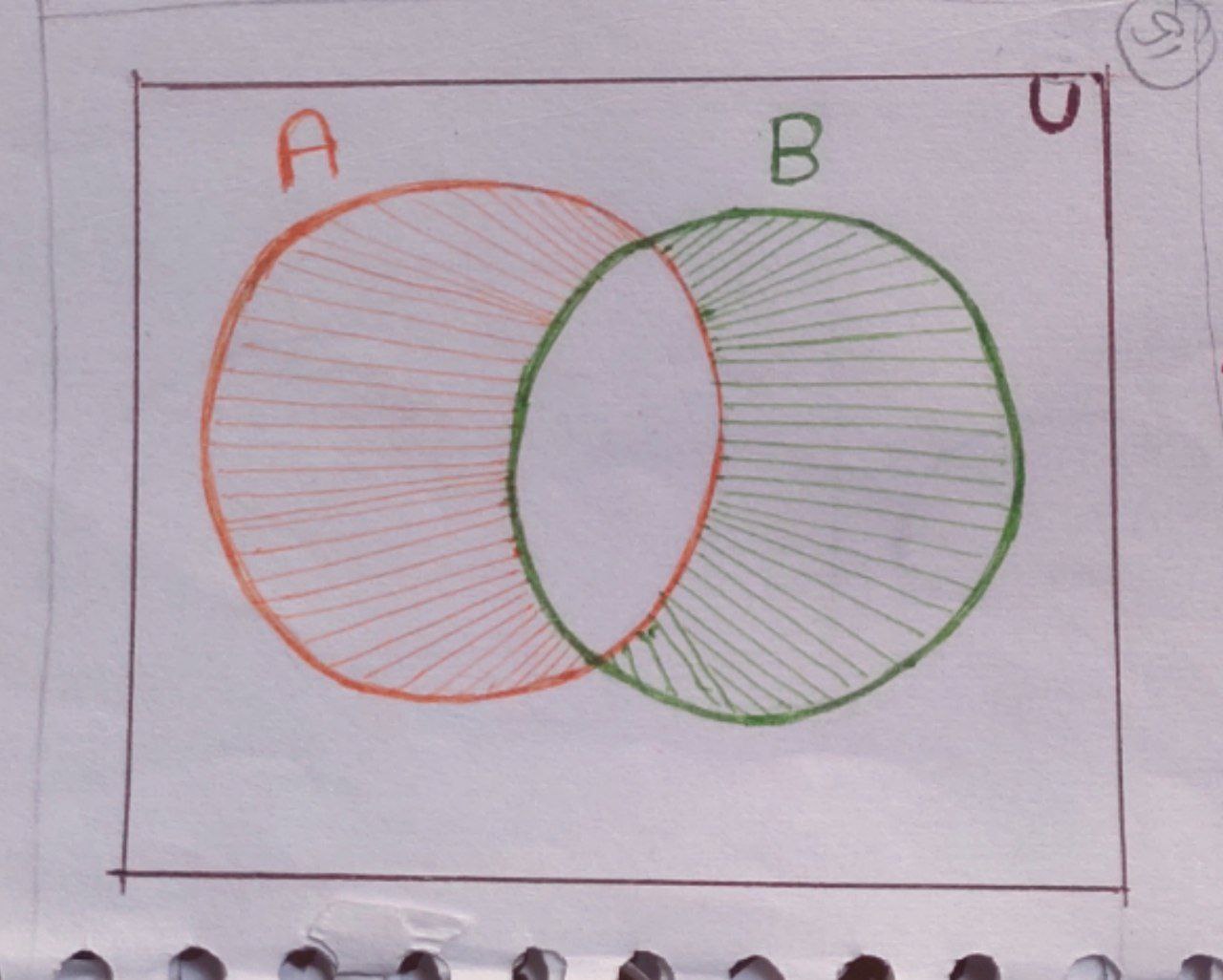
$ \boxed {\text{A} \triangle \text{B} = ({ \text{A} – \text{B}) \cup (\text{B} – \text{A})}} $
Now, $ \text{P} \triangle \text{Q} = \{ 1,2,3,4\} \triangle \{ 2,3,5,6\} $
$ \Rightarrow \text{P} \triangle \text{Q} = \{ 1, 4, 5,6 \} $
And, $ \text{R} \triangle \text{S} = \{ 1,3,7,8,9 \} \triangle \{ 2,4,9,10 \} $
$ \Rightarrow \text{R} \triangle \text{S} = \{ 1,2,3,4,7,8,10 \} $
Thus, $ ( \text{P} \triangle \text{Q}) \triangle ( \text{R} \triangle \text{S}) = \{ 1,4,5,6 \} \triangle \{ 1,2,3,4,7,8,10 \} $
$ \Rightarrow ( \text{P} \triangle \text{Q}) \triangle ( \text{R} \triangle \text{S}) = \{ 2,3,5,6,7,8,10 \} $
$\therefore$ The number of elements in $( \text{P} \triangle \text{Q}) \triangle (\text{R} \triangle \text{S})$ is $7.$
Correct Answer $: \text{B}$