Given that, area of rectangle ${ABCD} = 768 \; \text{cm}^{2}.$
Let the radius of semicircle be $`r\text{’} \; \text{cm}.$
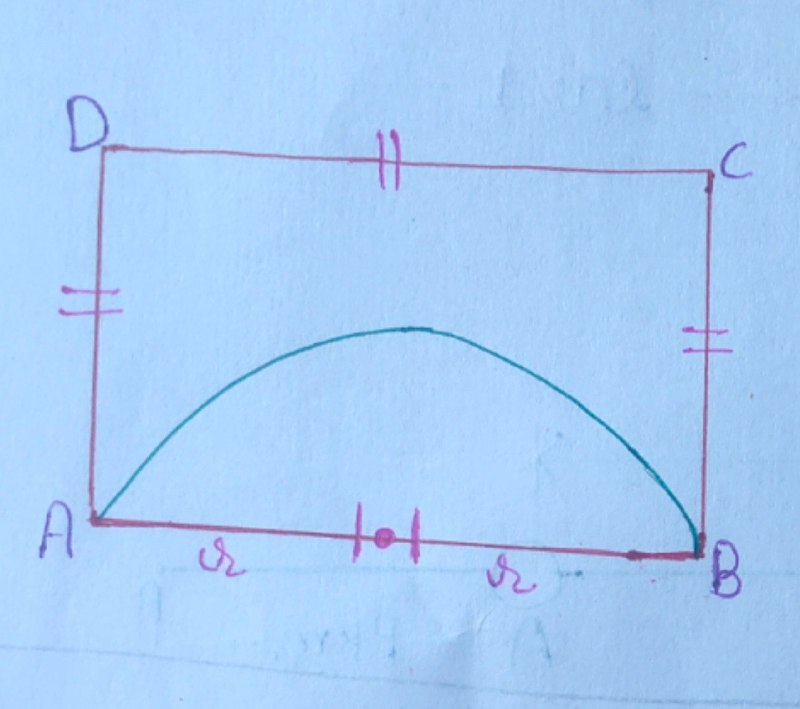
$\text{Area of semicircle} = \dfrac{\pi r^{2}}{2},$ where $`r\text{’}$ is the radius of semicircle.
$ \Rightarrow \frac{\pi r^{2}}{2} = 72 \pi $
$ \Rightarrow r^{2} = 144 $
$ \Rightarrow \boxed{r = 12 \; \text{cm}} $
$ \Rightarrow \boxed{ AB = 2r = 24 \; \text{cm}} $
$\text{Area of rectangle} = AB \times BC $
$ \Rightarrow 24 \; BC = 768 $
$ \Rightarrow BC = \frac{768}{24} $
$ \Rightarrow \boxed{ BC = 32 \; \text{cm}} $
A semicircular part is removed from the rectangle. The figure will be :
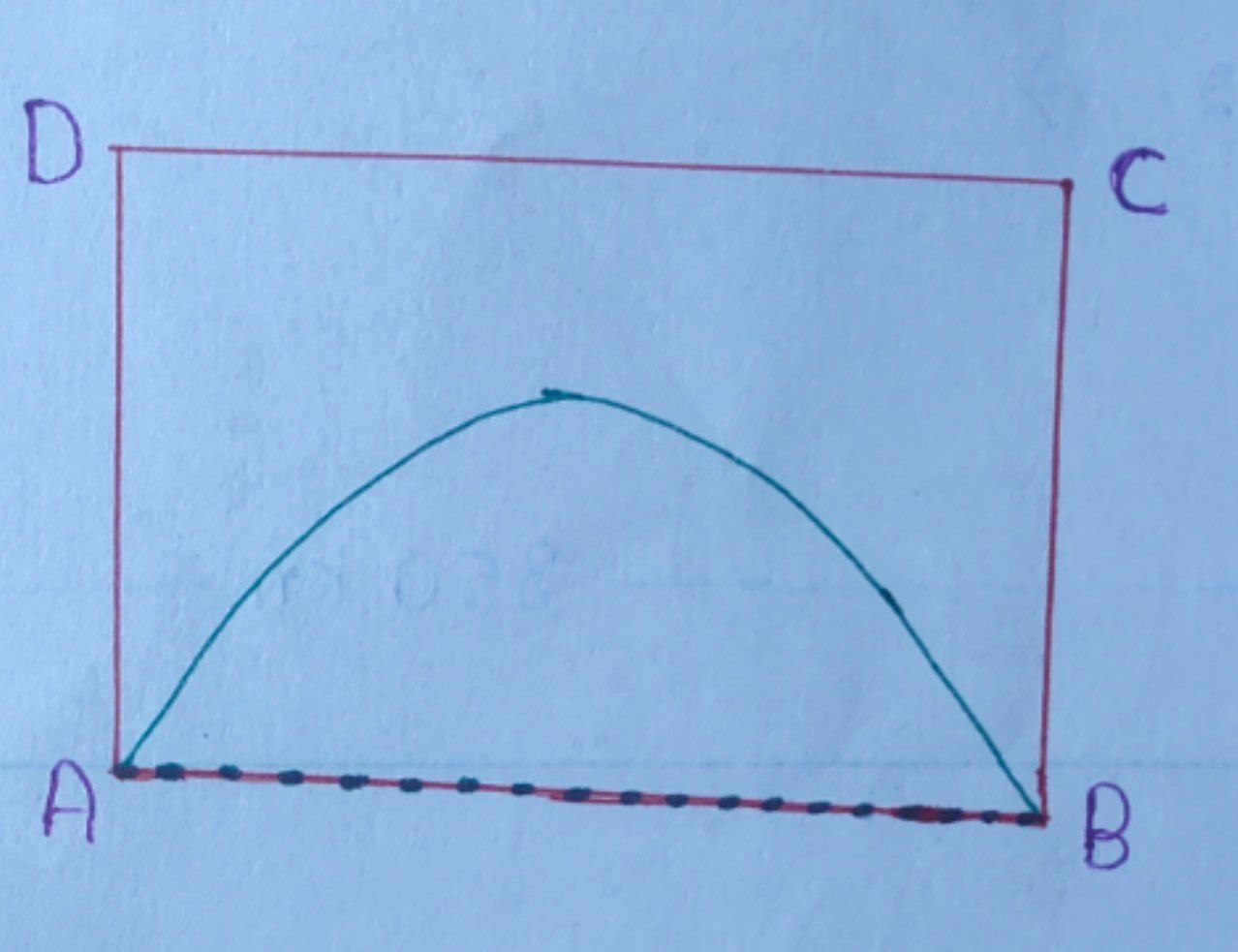
The perimeter of the remaining portion $ = AD + DC + BC + \text{arc} (AB) $
$\quad = 32 + 24 + 32 + $ Perimeter of semicircle
$\quad = 88 + \frac{2 \pi (12)} {2} \quad [\because \text{Perimeter of semicircle} = \frac {2 \pi r}{2} = \pi r] $
$ \quad = (88 + 12 \pi) \; \text{cm}. $
Correct Answer $: \text{D} $