Given that, $\triangle ABC$ has area $ = 32 \; \text{sq units.}$
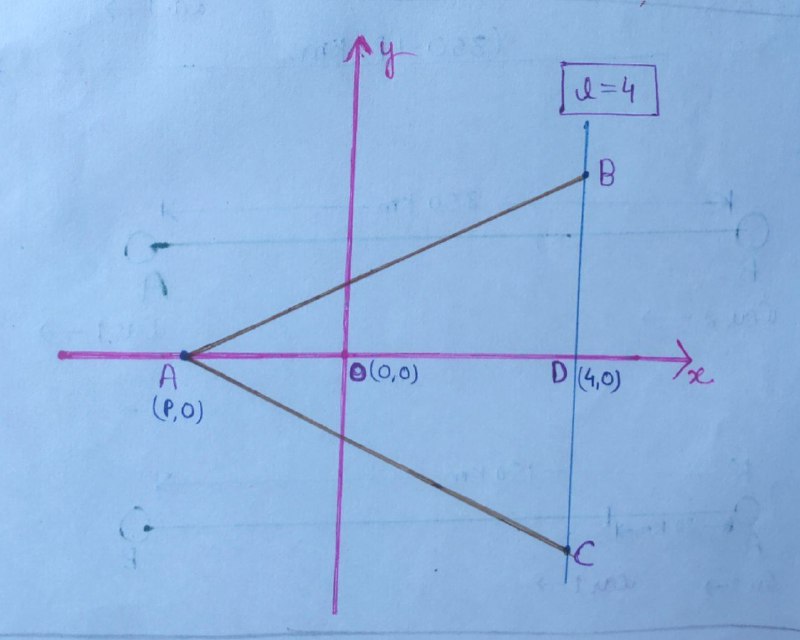
Length of $BC = 8 \; \text{units},$ and it lies on the line $x=4.$
Since we want the shortest distance possible between $A$ and the point $(0,0).$
So, we can assume point $A$ lie on the $x\text{-axis}$ and its coordinates be $(p,0).$
Since $|x_{1} – x_{2}|$ is the distance between the $x\text{-coordinates}$ of the two points.
So, the height of the $\triangle ABC:\; \boxed {AD = |p-4| \; \text{units}} $
$\text{The area of triangle} = \frac{1}{2} \times \text{Base} \times \text{Height} $
The area of $\triangle ABC = \frac{1}{2} \times 8 \times |p-4| $
$ \Rightarrow 4 \times |p-4| = 32 $
$ \Rightarrow |p-4| = 8 $
$ \Rightarrow p-4 = 8 \; (\text{or}) \; – (p-4) = 8 $
$ \Rightarrow \boxed{ p=12} \; (\text{or}) \; -p+4 = 8 \Rightarrow \boxed{p= -4} $
$\therefore$ The shortest possible distance between $A(p,0) = A(-4,0)$ and the point $O(0,0) = |-4-0| = |-4| = 4 \; \text{units.} $
Correct Answer $: \text{A}$
$\textbf{PS:}$ For any real number $x,$ the absolute value or modulus of $x$ is denoted by $|x|.$
$$|x| = \left\{\begin{matrix} x\;, & \text{if} \; x \geq 0 & \\ -x\;, & \text{if} \; x <0. & \end{matrix}\right.$$