Given that, $A,P,Q$ and $B$ lie on the same line such that $P,Q$ and $B$ are respectively, $100 \; \text{km}, 200 \; \text{km}$ and $300 \; \text{km}$ away from $A.$
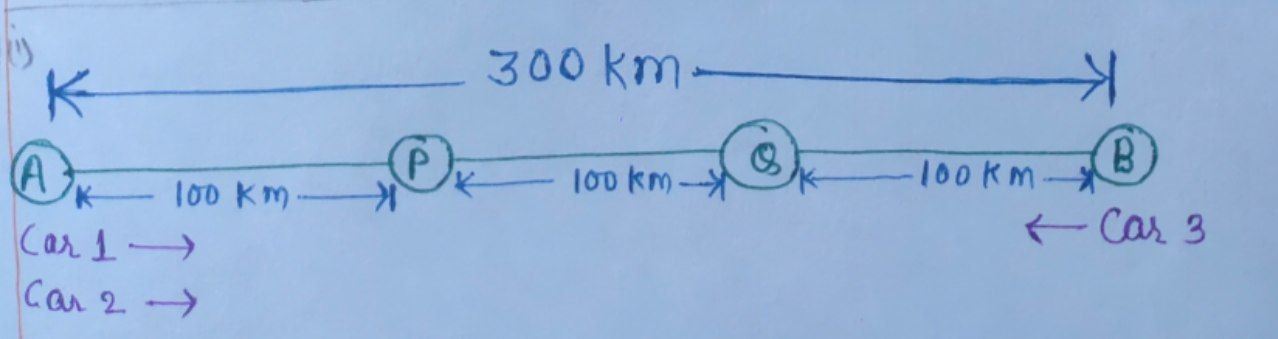
Let the speed of $\text{Car 1, Car 2}$ and $\text{Car 3}$ be $x,y$ and $z \; \text{km/hr}.$
After some time, $\text{Car 3}$ meets $\text{Car 1}$ at $Q.$

We know that, $ \boxed{\text{Speed} = \frac{\text{Distance}}{\text{Time}}} $
$ \Rightarrow \boxed{\text{Speed} \propto \text{Distance}} \text{(Time constant)} $
$ \Rightarrow \boxed{\frac{S_{1}}{S_{2}} = \frac{D_{1}}{D_{2}}} $
We can say that, if time is constant, speed is directly proportional to distance.
- Distance traveled by $\text{Car 1} = 200 \; \text{km} $
- Distance traveled by $ \text{Car 3} = 100 \; \text{km} $
So, $\frac{x}{z} = \frac{200}{100} $
$ \Rightarrow \frac{x}{z} = \frac{2}{1} $
$ \Rightarrow \boxed{x : z = 2 : 1} \quad \longrightarrow (1) $
After some time, $\text{Car 3}$ meets $\text{Car 2}$ at $P.$
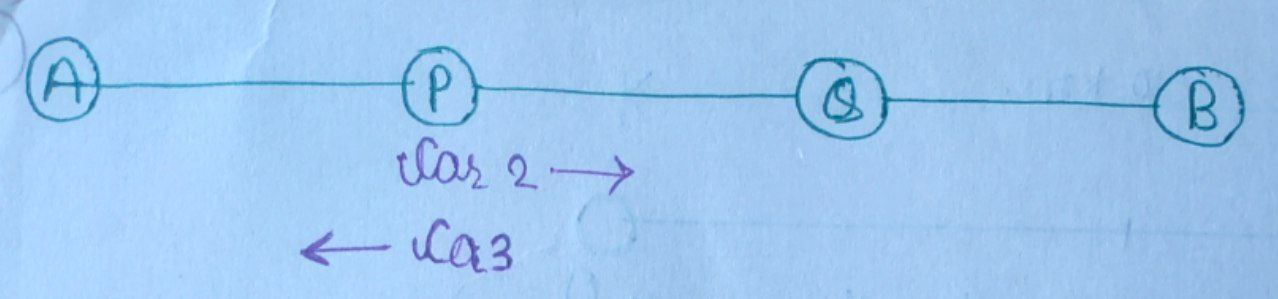
- Distance traveled by $\text{Car 2} = 100 \; \text{km} $
- Distance traveled by $ \text{Car 3} = 200 \; \text{km} $
So, $\frac{y}{z} = \frac{100}{200} $
$ \Rightarrow \frac{y}{z} = \frac{1}{2} $
$ \Rightarrow \boxed{y : z = 1 : 2} \quad \longrightarrow (2) $
Now, combine the ratios, from equation $(1),$ and $(2),$ we get.
- $ x:z = (2:1) \times 2 = 4:2 $
- $ y:z = (1:2) \times 1 = 1:2 $
- $x:y:z = 4:1:2 $
$\therefore$ The ratio of the speed of $\text{car2}$ to that of $\text{car1} = y:x = 1:4.$
Correct Answer $: \text{C}$