Given that, point $P$ lies between $A$ and $B$ such that the length of $BP$ is thrice that of $AP$. It means $\boxed{BP = 3 \; AP}$
Let the total distance be $`4d\text{’} \; \text{km}.$
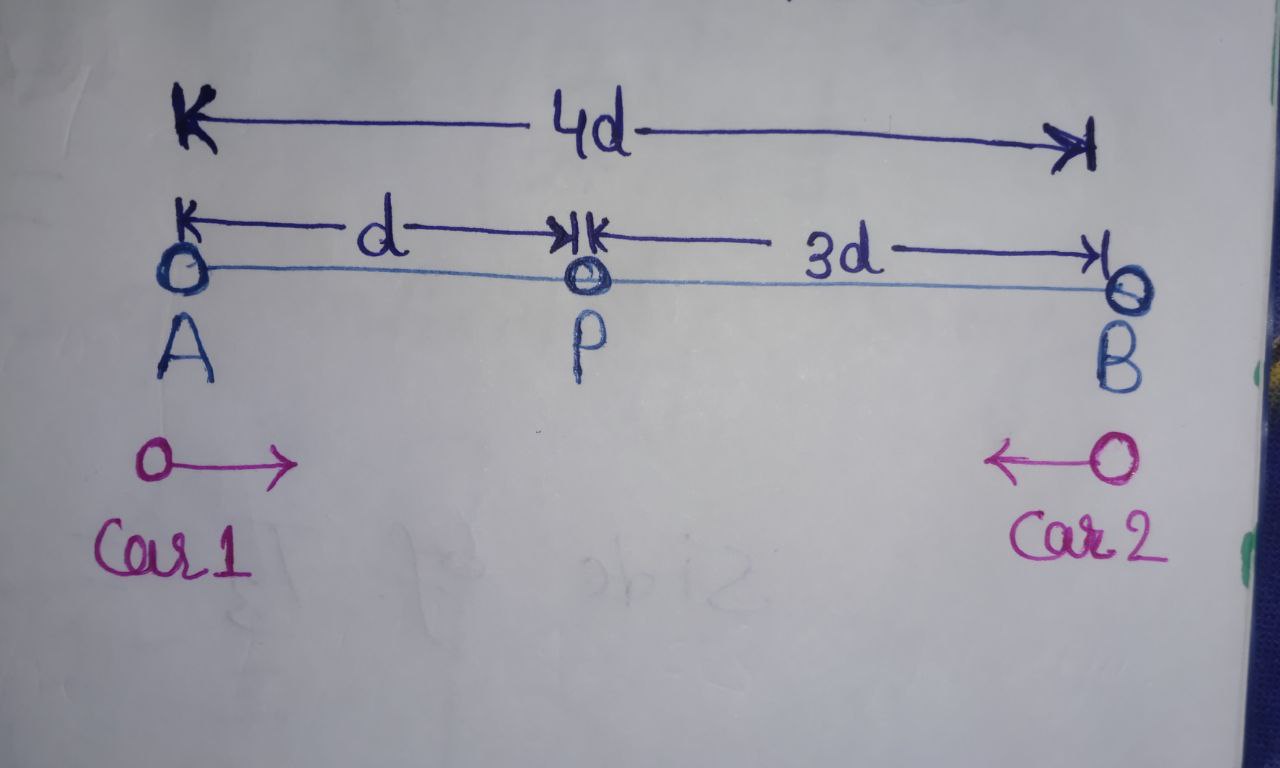
Let $\text{car 1}$ takes $`t\text{’} \; \text{hours}$ to reach point $P.$
So, $ \text{car 2}$ takes $`(t+1)\text{’} \; \text{hours}$ to reach point $P.$
The speed of $\text{car 2}$ is half that of $ \text{car 1.}$
Thus$, \text{S}_{\text{car 2}} = \frac{1}{2} \text{S}_{\text{car 1}}$
$ \Rightarrow \boxed {\text{S}_{\text{car 1}} = 2 \text{S}_{\text{car 2}}} \quad \longrightarrow (1)$
We know that, $ \text{Speed} = \frac{\text{Distance}}{\text{Time}}$
Now, the speed of $\text{car 1,}$ and $\text{car 2.}$
- $\text{S}_{\text{car 1}} = \frac{d}{t}$
- $\text{S}_{\text{car 2}} = \frac{3d}{t+1}$
Put the values in equation ${(1),}$ we get
$ \frac{d}{t} = 2 \left( \frac{3d}{t+1} \right)$
$ \Rightarrow \frac{1}{t} = \frac{6}{t+1}$
$ \Rightarrow t+1 = 6t $
$ \Rightarrow 5t = 1 $
$ \Rightarrow t = \frac {1}{5} \; \text{hours}$
$ \Rightarrow t = \frac{1}{5} \times 60 $
$ \Rightarrow t = 12 \; \text{minutes}$
$ \therefore$ The time taken by $ \text{car 1}$ to reach $P$ from $A$ is $12 \; \text{minutes}.$
Correct Answer $: 12$