Given that,
- $n (\text {U}) = 200 $
- $ n (\text {P}) = 105 $
- $ n ( \text {B}) = 134$
Let the number of students who like both pizza and burger be $m.$
And, let the number of students who like neither pizza nor burger be $n.$
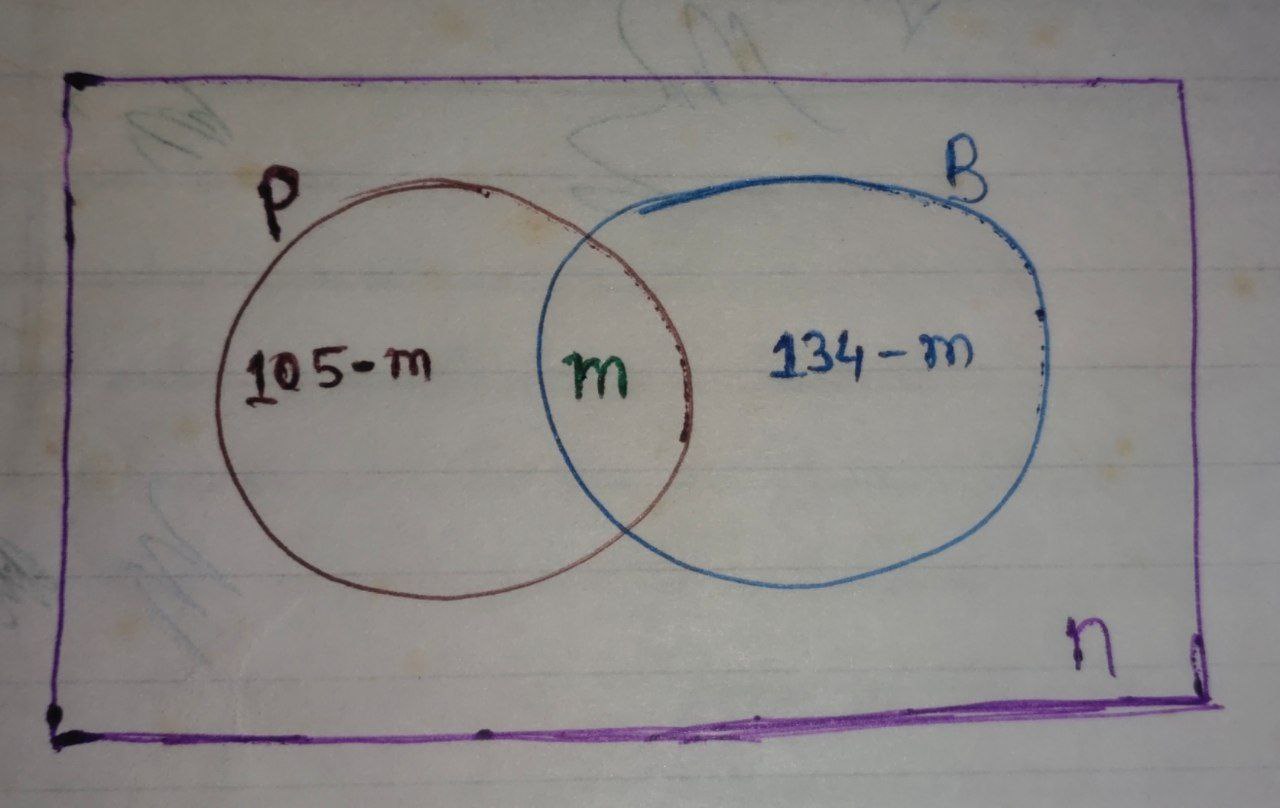
From the above Venn diagram,
$ ( 105-m) + m + (134-m) + n = 200 $
$ \Rightarrow – m + n = 200 – 239 $
$ \Rightarrow \boxed{m-n = 39} \quad \longrightarrow (1)$
$ \therefore $ The possible value of $(m , n)$ are $ (39,0), (40-1), \dots , (104,65), (105,66) $
So, the number of students who like only burger, should be in the range.
$ [134-105, 134-39] $
$ = [29,95] $
$\therefore$ From the given options, $93$ can be possible.
Correct Answer $:\text {A}$